슬라이딩 윈도우(Sliding Window) 알고리즘 패턴
윈도우(특정 범위)가 있을 때, 윈도우 내부 요소의 값을 이용하여 문제를 풀이하는 알고리즘이다.
- 배열이나 문자열같은 선형 구조에서 요소의 일정 범위값을 비교할 때, 사용하면 유용한 패턴이다.
- 투 포인터 패턴과 유사하다.
- 특정한 조건에 따라 window가 커지거나 닫히거나, 새로 생성될수도 있다.
예를 들어, 한 단어의 문자들 중 연속된 고유 문자의 길이가 가장 긴 부분을 출력할 때, 슬라이딩 윈도우와 같은 패턴을 사용할 수 있다.
프로세스
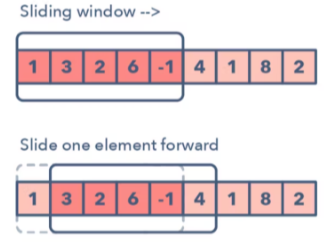
ex. [1, 3, 2, 6, -1, 4, 1, 8, 2] 라는 배열이 있는데, 연속적인 5개의 숫자의 합이 최대값을 구한다고 가정을 해본다.
[1, 3, 2, 6, -1], 4, 1, 8, 2 합 : 11
1, [3, 2, 6, -1, 4], 1, 8, 2 합 : 14
1, 3, [2, 6, -1, 4, 1], 8, 2 합 : 12
1, 3, 2, [6, -1, 4, 1, 8], 2 합 : 18
1, 3, 2, 6, [-1, 4, 1, 8, 2] 합 : 14이런 식으로 구해볼 수 있다. 지금은 배열이 짧아서 하나씩 구해볼 수 있지만, 배열이 30개, 연속적인 숫자 2개의 합을 구하라 하면 일일히 계산하는 것은 비효율적이다. 그러므로 공된 패턴을 통해 코드를 구현해야 한다.
개념
첫 번째로 1 + 3 + 2 + 6 + (-1) 를 계산하고
두 번째로 3 + 2 + 6 + (-1) + 4 를 계산하면 되는데, 여기서 중복적인 부분이 생기게 된다.
그럼 중복적인 경우를 코드로 구현한다면 처음 계산된 합에서 맨 앞 인덱스를 빼고, 마지막 인덱스를 더하여 계산하면 된다.
ex)
console.log(solution([1, 2, 5, 2, 8, 1, 5], 2)); // 10
console.log(solution([1, 2, 5, 2, 8, 1, 5], 4)); // 17
console.log(solution([4, 2, 1, 6], 1)); // 6
console.log(solution([4, 2, 1, 6, 2], 4)); // 13
console.log(solution([], 4)); // null안좋은 방식
const solution = (arr, N) => {
let p1 = 0;
let p2 = N - 1;
const newArr = [];
while (p2 < arr.length) {
newArr.push(arr.slice(p1, N + p1).reduce((sum, cur) => sum + cur), 0);
p1++;
p2++;
}
if (newArr.length === 0) return null;
return Math.max(...newArr);
};while문 안에 reduce로 반복을 돌기때문에 시간복잡도 O(N^2)이다. 이런 형태로는 포인터를 두개를 써서 얻는 이점도 없는 것 같다.
그래도 위와 같이 간단한 예제에서는 문제가 되지 않지만 방대한 길이의 배열, 방대한 양의 수만큼의 합을 구하게 된다면 굉장히 비효율적인 방식이 될 것이다. 이를 슬라이딩 윈도우 패턴을 통해 리팩토링 해보자.
슬라이딩 윈도우 패턴 적용
- 먼저 window에 0번 인덱스부터 N번 인덱스 까지의 합을 저장한다.
- 이제 N번 인덱스부터 탐색을 진행하고, window에 현재 인덱스를 더하고, 현재 인덱스의 -N을 한 인덱스를 빼준다.
- 처음 더한 합에서 첫번재 수를 빼고 다음 루프의 첫번째 수를 더하기만 하면 된다.
- 계산 후, 최대값 비교를 한다.
const solution = (arr, N) => {
let window = 0;
let maxSum = 0;
if (arr.length < N) return null;
for (let i = 0; i < N; i++) // N가지 숫자를 window에 더한다
window += arr[i];
maxSum = window; // maxSum에 window를 복사해 보관해두고
for (let i = N; i < arr.length; i++) { // window까지 더했던 인덱스의 다음인덱스를 시작점으로 loop
window += arr[i] - arr[i - N]; // 바로 앞 인덱스 값은 빼고, 바로 다음 인덱스 값은 더한다
maxSum = Math.max(maxSum, window); // maxSum과 window를 비교해서 더 큰값을 maxSum에 할당한다.
}
return maxSum;
};solution([2, 6, 9, 2, 1, 8, 5, 6, 3], 3) 의 동작순서를 보면
//N = 3
//for (let i = 0; i < N; i++) {
// maxSum += arr[i];
//}
//tempSum = maxSum;
[2, 6, 9, 2, 1, 8, 5, 6, 3] //MaxSum = 17, tempSum = 17
+ + +
---------------------------------------------------------------
//for (let i = N; i < arr.length; i++) {
// tempSum = tempSum - arr[i - N] + arr[i];
// maxSum = Math.max(maxSum, tempSum);
//}
// i = N(값은 3) 일때
/*-------------------------------------------------------------*/
- //tempSum - arr[3 - 3]
[2, 6, 9, 5, 6, 8, 1, 2, 3] //MaxSum = 20, tempSum = 20
+ // + arr[3]
/*-------------------------------------------------------------*/
/*-------------------------------------------------------------*/
- //tempSum - arr[4 - 3]
[2, 6, 9, 5, 6, 8, 1, 2, 3] //MaxSum = 20, tempSum = 20
+ // + arr[4]
/*-------------------------------------------------------------*/
/*-------------------------------------------------------------*/
- //tempSum - arr[5 - 3]
[2, 6, 9, 5, 6, 8, 1, 2, 3] //MaxSum = 20, tempSum = 19
+ // + arr[5]
/*-------------------------------------------------------------*/
.
.
.
/*-------------------------------------------------------------*/
- //tempSum - arr[8 - 3]
[2, 6, 9, 5, 6, 8, 1, 2, 3] //MaxSum = 20, tempSum = 6
+ // + arr[8]
/*-------------------------------------------------------------*/
// maxSum인 20을 리턴한다시간복잡도는 O(N)이다.
장점
- 슬라이딩 윈도우는 고정적인 범위를 탐색할 때, 유용하다.
- 중복으로 연산을 제거하면서 효율을 높일 수 있다.
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] (알고리즘 패턴) 투 포인터(다중 포인터) (0) | 2023.03.24 |
|---|---|
| [Algorithm] 유클리드 호제법 (최대공약수 & 최소공배수 구하기) (0) | 2023.03.24 |
| [Algorithm] Segment Tree (구간 트리) (0) | 2023.03.23 |
| [Algorithm] KMP 알고리즘 (Knuth-Morris-Pratt Algorithm) (0) | 2023.03.23 |
| [Algorithm] 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2023.03.23 |



댓글