 [Algorithm] (알고리즘 패턴) 슬라이딩 윈도우(Sliding Window)
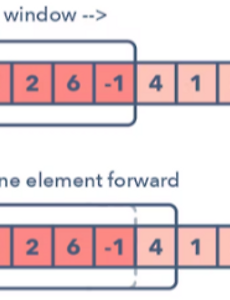
슬라이딩 윈도우(Sliding Window) 알고리즘 패턴 윈도우(특정 범위)가 있을 때, 윈도우 내부 요소의 값을 이용하여 문제를 풀이하는 알고리즘이다. 배열이나 문자열같은 선형 구조에서 요소의 일정 범위값을 비교할 때, 사용하면 유용한 패턴이다. 투 포인터 패턴과 유사하다. 특정한 조건에 따라 window가 커지거나 닫히거나, 새로 생성될수도 있다. 예를 들어, 한 단어의 문자들 중 연속된 고유 문자의 길이가 가장 긴 부분을 출력할 때, 슬라이딩 윈도우와 같은 패턴을 사용할 수 있다. 프로세스 ex. [1, 3, 2, 6, -1, 4, 1, 8, 2] 라는 배열이 있는데, 연속적인 5개의 숫자의 합이 최대값을 구한다고 가정을 해본다. [1, 3, 2, 6, -1], 4, 1, 8, 2 합 : 11 1..
2023. 3. 24.
[Algorithm] (알고리즘 패턴) 슬라이딩 윈도우(Sliding Window)
슬라이딩 윈도우(Sliding Window) 알고리즘 패턴 윈도우(특정 범위)가 있을 때, 윈도우 내부 요소의 값을 이용하여 문제를 풀이하는 알고리즘이다. 배열이나 문자열같은 선형 구조에서 요소의 일정 범위값을 비교할 때, 사용하면 유용한 패턴이다. 투 포인터 패턴과 유사하다. 특정한 조건에 따라 window가 커지거나 닫히거나, 새로 생성될수도 있다. 예를 들어, 한 단어의 문자들 중 연속된 고유 문자의 길이가 가장 긴 부분을 출력할 때, 슬라이딩 윈도우와 같은 패턴을 사용할 수 있다. 프로세스 ex. [1, 3, 2, 6, -1, 4, 1, 8, 2] 라는 배열이 있는데, 연속적인 5개의 숫자의 합이 최대값을 구한다고 가정을 해본다. [1, 3, 2, 6, -1], 4, 1, 8, 2 합 : 11 1..
2023. 3. 24.