삽입 정렬 (Insertion Sort)
손 안의 카드를 정렬하는 방법과 유사하다.
Insertion Sort는 Selection Sort와 유사하지만, 좀 더 효율적인 정렬 알고리즘이다.
Insertion Sort는 2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입 하여 정렬하는 알고리즘이다.
Selection Sort와 Insertion Sort는 k번째 반복 이후, 첫번째 k 요소가 정렬된 순서로 온다는 점에서 유사하다. 하지만, Selection Sort는 k+1번째 요소를 찾기 위해 나머지 모든 요소들을 탐색한다. 하지만 Insertion Sort는 k+1번째 요소를 배치하는 데 필요한 만큼의 요소만 탐색하기 때문에 훨씬 효율적으로 실행된다는 차이가 있다.
최선의 경우 O(N)이라는 엄청나게 빠른 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다.
프로세스
- 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
- 즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
- 처음 Key 값은 두 번째 자료부터 시작한다.
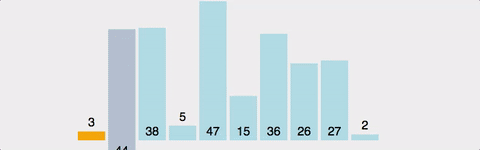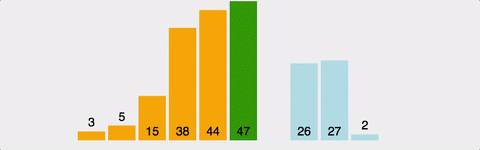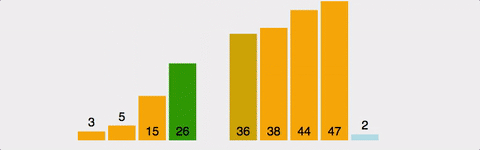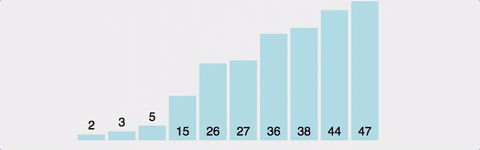
ex)

- 1회전: 두 번째 자료인 5를 Key로 해서 그 이전의 자료들과 비교한다.
- Key 값 5와 첫 번째 자료인 8을 비교한다. 8이 5보다 크므로 8을 5자리에 넣고 Key 값 5를 8의 자리인 첫 번째에 기억시킨다.
- 2회전: 세 번째 자료인 6을 Key 값으로 해서 그 이전의 자료들과 비교한다.
- Key 값 6과 두 번째 자료인 8을 비교한다. 8이 Key 값보다 크므로 8을 6이 있던 세 번째 자리에 기억시킨다.
- Key 값 6과 첫 번째 자료인 5를 비교한다. 5가 Key 값보다 작으므로 Key 값 6을 두 번째 자리에 기억시킨다.
- 3회전: 네 번째 자료인 2를 Key 값으로 해서 그 이전의 자료들과 비교한다.
- Key 값 2와 세 번째 자료인 8을 비교한다. 8이 Key 값보다 크므로 8을 2가 있던 네 번째 자리에 기억시킨다.
- Key 값 2와 두 번째 자료인 6을 비교한다. 6이 Key 값보다 크므로 6을 세 번째 자리에 기억시킨다.
- Key 값 2와 첫 번째 자료인 5를 비교한다. 5가 Key 값보다 크므로 5를 두 번째 자리에 넣고 그 자리에 Key 값 2를 기억시킨다.
- 4회전: 다섯 번째 자료인 4를 Key 값으로 해서 그 이전의 자료들과 비교한다.
- Key 값 4와 네 번째 자료인 8을 비교한다. 8이 Key 값보다 크므로 8을 다섯 번째 자리에 기억시킨다.
- Key 값 4와 세 번째 자료인 6을 비교한다. 6이 Key 값보다 크므로 6을 네 번째 자리에 기억시킨다.
- Key 값 4와 두 번째 자료인 5를 비교한다. 5가 Key 값보다 크므로 5를 세 번째 자리에 기억시킨다.
- Key 값 4와 첫 번째 자료인 2를 비교한다. 2가 Key 값보다 작으므로 4를 두 번째 자리에 기억시킨다.
function insertionSort(arr) {
for(let index = 1 ; index < arr.length ; index++){ // 1.
int currentVal = arr[index];
int prev = index - 1;
while( (prev >= 0) && (arr[prev] > currentVal) ) { // 2.
arr[prev + 1] = arr[prev];
prev--;
}
arr[prev + 1] = currentVal; // 3.
}
}- 첫 번째 원소 앞(왼쪽)에는 어떤 원소도 갖고 있지 않기 때문에, 두 번째 위치(index)부터 탐색을 시작한다. currentVal에 임시로 해당 위치(index) 값을 저장하고, prev에는 해당 위치(index)의 이전 위치(index)를 저장한다.
- 이전 위치(index)를 가리키는 prev가 음수가 되지 않고, 이전 위치(index)의 값이 '1'번에서 선택한 값보다 크다면, 서로 값을 교환해주고 prev를 더 이전 위치(index)를 가리키도록 한다.
- '2'번에서 반복문이 끝나고 난 뒤, prev에는 현재 currentVal 값보다 작은 값들 중 제일 큰 값의 위치(index) 를 가리키게 된다. 따라서, (prev+1)에 temp 값을 삽입해준다.
시간복잡도
| 평균 | 최선 | 최악 |
| Θ(n^2) | Ω(n) | O(n^2) |
- 최선의 경우(정렬이 되어있는 경우)
- 비교 횟수
- 이동 없이 1번의 비교만 이루어진다.
- 외부 루프: (n - 1)번
- 이미 정렬이 되어있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
- 비교 횟수
Best T(n) = Ω(n)
- 최악의 경우(입력 자료가 역순일 경우)
- 비교 횟수
- 외부 루프 안의 각 반복마다 i번의 비교 수행
- 외부 루프: (n - 1) + (n - 2) + … + 2 + 1 = n(n - 1) / 2 = O(n^2)
- 교환 횟수
- 외부 루프의 각 단계마다 (i + 2)번의 이동 발생
- n(n - 1) / 2 + 2(n - 1) = (n^2 + 3n - 4) / 2 = O(n^2)
- 비교 횟수
Worst T(n) = O(n^2)
공간복잡도
주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
장점
- 알고리즘이 단순하다.
- 대부분의 원소가 이미 정렬되어 있는 경우, 알고리즘이 매우 간단하므로 다른 복잡한 정렬보다 매우 효율적일 수 있다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
- 안정 정렬(Stable Sort) 이다.
- Selection Sort나 Bubble Sort과 같은 O(n^2) 알고리즘에 비교하여 상대적으로 빠르다.
단점
- 평균과 최악의 시간복잡도가 O(n^2)으로 비효율적이다.
- 비교적 많은 데이터들의 이동을 포함한다.
- Bubble Sort와 Selection Sort와 마찬가지로, 배열의 길이가 길어질수록 비효율적이다.
정렬 알고리즘 시간복잡도 비교

- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] 병합 정렬 (Merge Sort) (0) | 2023.02.27 |
|---|---|
| [Algorithm] 퀵 정렬 (Quick Sort) (0) | 2023.02.27 |
| [Algorithm] 선택 정렬 (Selection Sort) (0) | 2023.02.27 |
| [Algorithm] 거품 정렬 (Bubble Sort) (0) | 2023.02.27 |
| [Algorithm] 기본 수학 이론 - 점화식 (0) | 2023.02.13 |




댓글