퀵 정렬 (Quick Sort)
Quick Sort은 분할 정복(divide and conquer) 방법 을 통해 주어진 배열을 정렬한다.
* [분할 정복(divide and conquer) 방법]
큰 문제를 작은 문제 단위로 쪼개면서 해결해나가는 방식.
문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
Quick Sort은 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법이다. 또한, 합병 정렬(Merge Sort)과 달리 Quick Sort는 배열을 비균등하게 분할한다.
프로세스
- 배열 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
- 피벗을 기준으로 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 배열을 둘로 나눈다. 이렇게 배열을 둘로 나누는 것을 분할(Divide) 이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
- 분할된 두 개의 작은 배열에 대해 재귀(Recursion)적으로 이 과정을 반복한다.
- 피벗을 제외한 왼쪽 배열과 오른쪽 배열을 다시 정렬한다.
- 부분 배열에서도 다시 피벗을 정하고, 피벗을 기준으로 2개의 부분 배열로 나누는 과정을 반복한다.
- 배열의 크기가 0이나 1이 될 때까지 반복한다.
- 재귀 호출이 한 번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.


ex)

- 피벗 값을 입력 리스트의 첫 번째 데이터로 한다. (다른 임의의 값이어도 상관없다.)
- 2개의 인덱스 변수(low, high)를 이용해서 리스트를 두 개의 부분 리스트로 나눈다.
- 1회전: 피벗이 5인 경우,
- low는 왼쪽에서 오른쪽으로 탐색해가다가 피벗보다 큰 데이터(8)을 찾으면 멈춘다.
- high는 오른쪽에서 왼쪽으로 탐색해가다가 피벗보다 작은 데이터(2)를 찾으면 멈춘다.
- low와 high가 가리키는 두 데이터를 서로 교환한다.
- 이 탐색-교환 과정은 low와 high가 엇갈릴 때까지 반복한다.
- 2회전: 피벗(1회전의 왼쪽 부분리스트의 첫 번째 데이터)이 1인 경우,
- 위와 동일한 방법으로 반복한다.
- 3회전: 피벗(1회전의 오른쪽 부분리스트의 첫 번째 데이터)이 9인 경우,
- 위와 동일한 방법으로 반복한다.
단계 정리
하나의 리스트를 피벗(pivot)을 기준으로 두 개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
퀵 정렬은 다음의 단계들로 이루어진다.
- 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 재귀적 호출(순환 호출) 을 이용하여 다시 분할 정복 방법을 적용한다.
// 퀵 정렬 (재귀하는 부분)
var quickSort = function(array, left, right) {
if (left >= right) return;
// partition 함수를 호출하여 피벗을 기준으로 배열을 비균등 분할 - 분할(Divid)
const pivot = partition(array, left, right);
// 피벗은 제외한 2개의 부분 배열을 대상으로 순환 호출
quickSort(array, left, pivot - 1); // (left ~ 피벗 바로 앞) 앞쪽 부분 리스트 정렬 - 정복(Conquer)
quickSort(array, pivot + 1, right); // (피벗 바로 뒤 ~ right) 뒤쪽 부분 리스트 정렬 - 정복(Conquer)
}- 분할(Divide) : 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
- 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
// 분할 (정렬하는 부분)
// 2개의 비균등 배열 array[left ... pivot-1]와 array[pivot+1 ... right]의 합병 과정
// (실제로 숫자들이 정렬되는 과정)
var partition = function(array, left, right) {
/*
// 최악의 경우, 개선 방법
const mid = (left + right) / 2;
array = swap(array, left, mid);
*/
const pivot = array[left]; // 가장 왼쪽값을 피벗으로 설정
const low = left, high = right;
// low와 high가 교차할 때까지 반복(low < high)
while (low < high) {
// array[low]가 피벗보다 작으면 계속 low를 증가
while (high <= right && pivot > array[low]) ++low;
// array[high]가 피벗보다 크면 계속 high를 감소
while (high >= left && pivot < array[high]) --high;
// 만약 low와 high가 교차하지 않았으면 array[low]와 array[high]를 교환
if (low < high) array = swap(array, low, high);
}
// low와 high가 교차했으면 array[left]와 array[high]를 교환
array = swap(array, left, high);
// 피벗의 위치인 high를 반환
return high;
}
// 데이터 교환
function swap(array, lhs, rhs) {
const temp = array[lhs];
array[lhs] = array[rhs];
array[rhs] = temp;
return array;
}개선점
partition() 함수에서 피벗 값이 최소나 최대값으로 지정되어 파티션이 나누어지지 않았을 때, O(n^2)에 대한 시간복잡도를 가진다.
즉, 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있으면 O(n^2)의 시간복잡도를 가진다. 이때, 배열에서 가장 앞에 있는 값과 중간값을 교환해준다면 확률적으로나마 시간복잡도 O(nlog₂n)으로 개선할 수 있다.
하지만, 이 방법으로 개선한다해도 Quick Sort의 최악의 시간복잡도가 O(nlog₂n)가 되는 것은 아니다.
시간복잡도
| 평균 | 최선 | 최악 |
| Θ(nlog₂n) | Ω(nlog₂n) | O(n^2) |
최선의 경우(Best cases) : T(n) = Ω(nlog₂n)
- 비교 횟수 (log₂n)
- 순환 호출의 깊이
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k) 했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n) 임을 알 수 있다.
- 순환 호출의 깊이
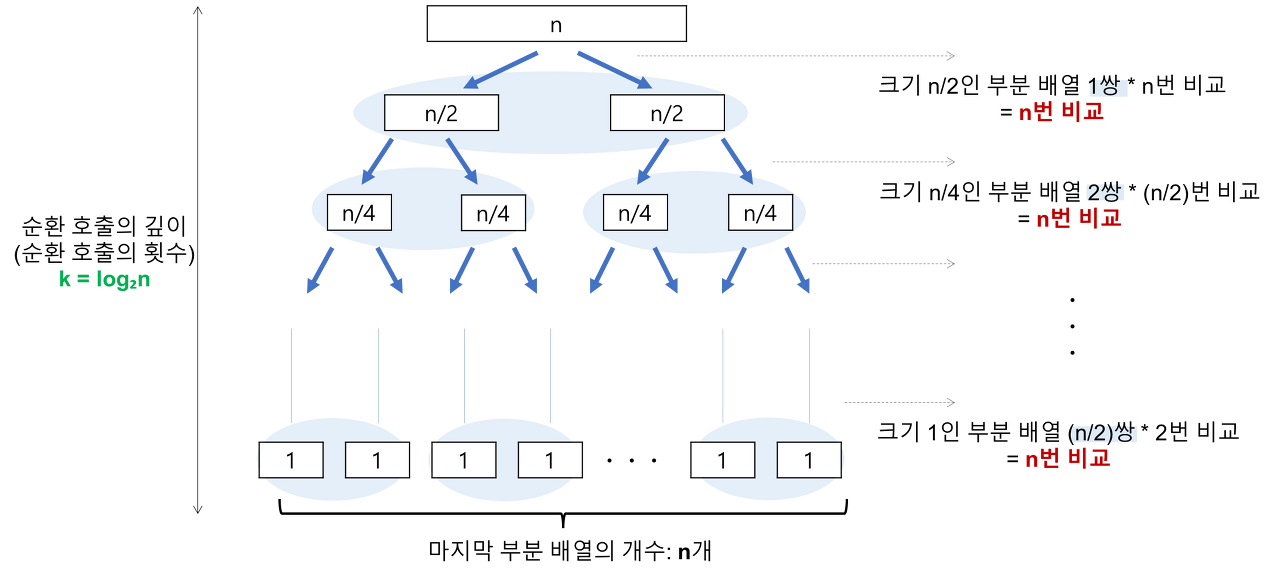
- 각 순환 호출 단계의 비교 연산 (평균 n번)
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
- 이동 횟수
- 비교 횟수보다 적으므로 무시할 수 있다.
따라서, 최선의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = Ω(nlog₂n)가 된다.
최악의 경우(Worst cases) : T(n) = O(n^2)
최악의 경우는 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있는 경우다.
배열이 계속 불균형하게 나누어지는 경우 (특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우)
- 비교 횟수 (n)
- 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n 임을 알 수 있다.

- 각 순환 호출 단계의 비교 연산 (평균 n번)
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
- 이동 횟수
- 비교 횟수보다 적으므로 무시할 수 있다.
따라서, 최악의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = O(n^2)다.
평균의 경우(Average cases) : T(n) = Θ(nlog₂n)
- 시간 복잡도가 Θ(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 퀵 정렬이 불필요한 데이터의 이동을 줄이고, 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문이다.
공간복잡도
주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 Θ(n)이다.
장점
- 속도가 빠르다
- 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.
단점
- 불안정 정렬(Unstable Sort) 이다.
- 정렬된 배열에 대해서는 Quick Sort의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
- 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때, 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
- ex) 배열 내의 몇 개의 데이터 중에서 크기순으로 중간 값(medium)을 피벗으로 선택한다.
정렬 알고리즘 시간복잡도 비교
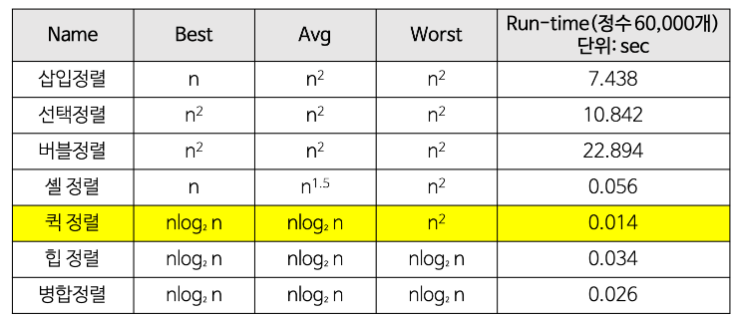
- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2023.02.27 |
|---|---|
| [Algorithm] 병합 정렬 (Merge Sort) (0) | 2023.02.27 |
| [Algorithm] 삽입 정렬 (Insertion Sort) (0) | 2023.02.27 |
| [Algorithm] 선택 정렬 (Selection Sort) (0) | 2023.02.27 |
| [Algorithm] 거품 정렬 (Bubble Sort) (0) | 2023.02.27 |




댓글