
그래프와 완전탐색
자료구조에서 말하는 그래프는 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한다.
직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있고, 간접적인 관계가 있는 경우 몇 개의 점과 선에 걸쳐 이어진다.
하나의 점을 정점(vertex)라고 표현하고 하나의 선은 간선(edge)라고 표현한다.
그래프의 탐색은 하나의 정점에서 시작하여 그래프의 모든 정점들을 한 번씩 방문(탐색)하는 것이 목적이고 이를 완전탐색이라 부르기도 한다. 모든 정점 탐색 방법에는 여러 가지가 있다. 그 중 DFS가 있다.

위 그림과 같은 그래프가 있다고 가정하겠다. 이 그래프를 어떤 방법으로 완전 탐색하냐에 따라 방문하는 순서가 달라진다.
DFS(Depth-First Search) 깊이 우선 탐색
루트 노드 혹은 임의 노드에서 다음 브랜치로 넘어가기 전에, 해당 브랜치를 모두 탐색하는 방법
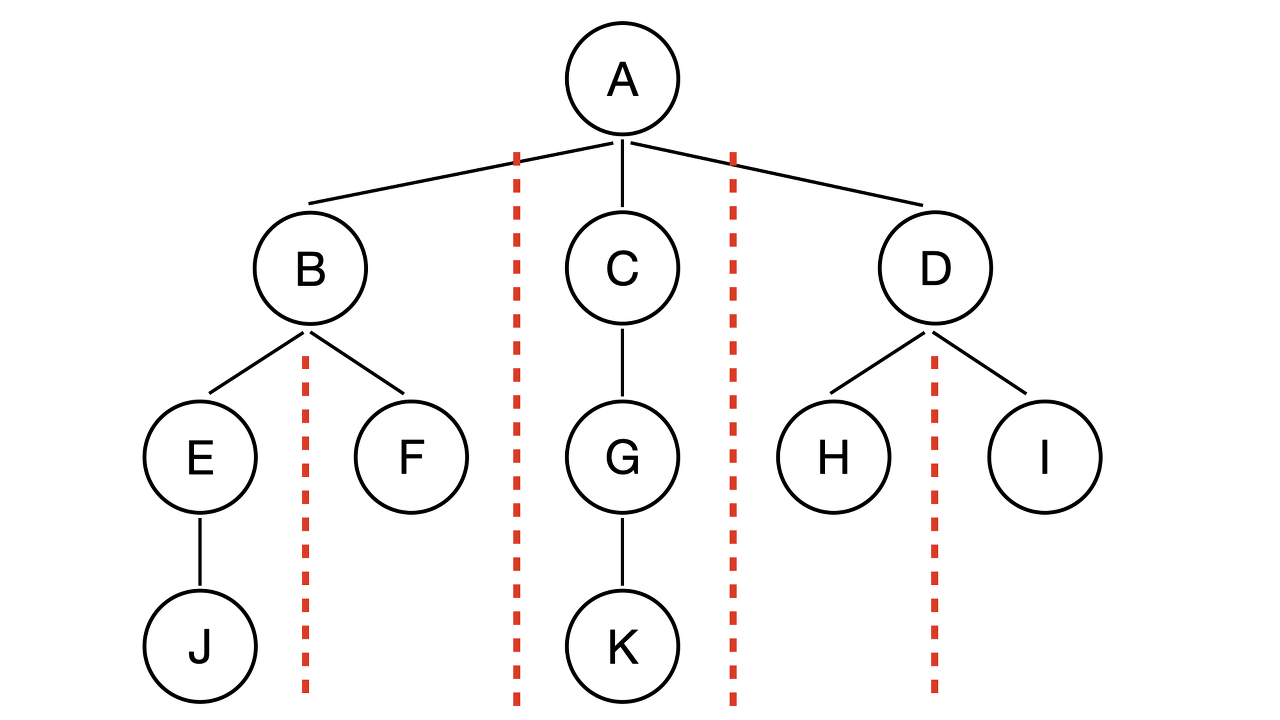
방문 순서부터 말하면 A-B-E-J-F-C-G-K-D-H-I 이다.
DFS는 하나의 경로를 아래까지 탐색한 후 그 다음 경로로 넘어간다. 전체적으로 보면 위에서 아래로 깊게 탐색이 진행된다.
스택 or 재귀함수를 통해 구현한다.
- 모든 경로를 방문해야 할 경우 사용에 적합

Ex) 스택을 이용한 구현
const dfs = (graph, startNode) => {
let visited = []; // 탐색한 노드를 담기 위한 배열 생성
let stack = []; // 탐색을 위한 스택 배열 생성
stack.push(startNode); // 탐색 시작
while(stack.length > 0){ // 스택이 비워질 때까지 반복
let node = stack.pop(); // 스택의 가장 마지막 노드를 뽑는다
if(!visited.includes(node.value)){ // 그 노드를 탐색한 적이 없다면!!
visited.push(node); // 탐색 배열에 추가
stack = [...graph[node], ...stack]; // 해당 노드의 자식 노드들을 스택에 담는다.
}
}
return visited;
}시간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(V+E)
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] Tail Recursion (꼬리 재귀) (0) | 2023.03.19 |
|---|---|
| [Algorithm] Disjoint Set의 표현: Union-Find (합집합 찾기) (0) | 2023.03.17 |
| [Algorithm] 완전 탐색 - 백트래킹(Backtracking), 깊이 우선 탐색(DFS. Depth-first search) (0) | 2023.03.13 |
| [Algorithm] BFS (너비 우선 탐색. Breadth-first search) (0) | 2023.03.13 |
| [Algorithm] 완전 탐색 - 브루트 포스(brute force), 너비 우선 탐색(BFS. Breadth-first search) (0) | 2023.03.13 |



댓글