Disjoint Set (서로소 집합)
'Disjoint set'는 공통 원소가 없는 부분 집합들이다.
어떤 교양 대면 수업에 여러 학과 사람들이 모여있다고 해보자. 이때 교수님이 갑자기 같은 과 사람들끼리 조를 만들라고 한다. 그럼 학생들은 이리 저리 돌아다니다가 같은 과 사람을 찾으면 팀을 이뤄 같이 움직이게 될 것이다. 그리고 팀끼리도 같은 과인 것을 확인하면 두 팀은 합쳐진다. 만들어진 조들은 공통 원소가 없는 부분 집합들, disjoint set이 된다.
이 상황을 자료구조로 표현한 것이, 즉, disjoint set에 대한 정보를 저장하고 조작하는 자료 구조가 'Union-Find'다.
Union-Find 알고리즘 (합집합 찾기)
- 대표적인 그래프 알고리즘으로 합집합 찾기라고도 불리며, 서로소 집합 (서로 중복되지 않고 공통 원소가 없는 부분 집합)을 표현할 때 사용하는 알고리즘이다.
- 주로 크루수칼 알고리즘과 함께 사용되며, 주로 트리(Tree) 구조를 이용하여 구현하게 된다.
- 여러개의 노드가 존재할 때, 두 개의 노드가 같은 그래프에 속하는지 판별하는 알고리즘
트리를 이용한 Union-Find
Union-Find를 구현하기 위해서는 세 가지 연산이 필요하다.
- 초기화 : n개의 원소가 각각의 집합에 포함되어 있도록 초기화한다.
- 합치기(union) 연산 : 두 원소 a, b가 주어질 때 이들이 속한 두 집합을 하나로 합친다.
- 찾기(find) 연산 : 어떤 원소 a가 주어질 때 이 원소가 속한 집합을 반환한다.
Union-Find 는 주로 트리 자료구조를 사용해서 한 집합에 속하는 원소들을 하나의 트리로 묶어준다.
프로세스

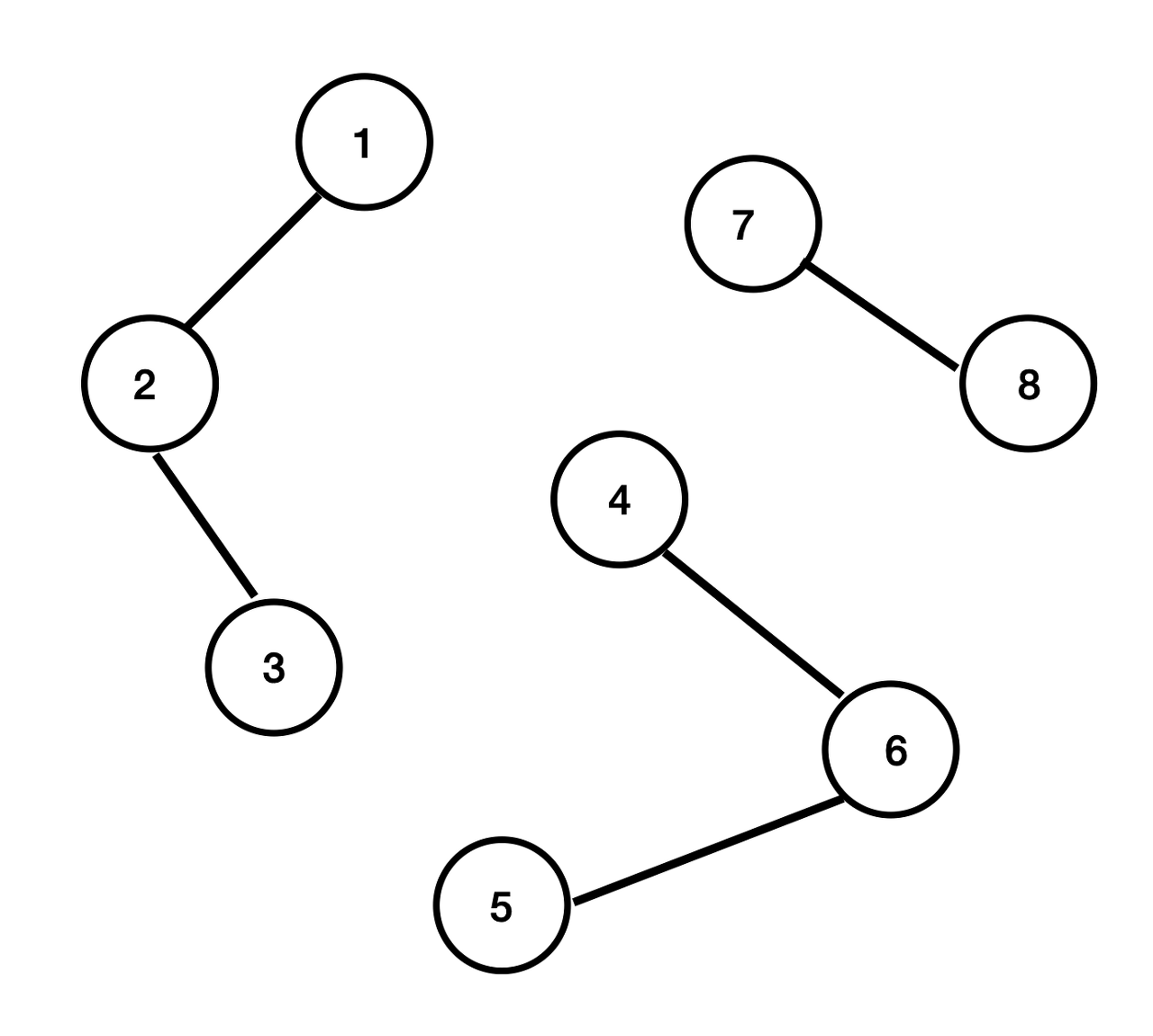
처음 8개의 노드가 무분별하게 존재한다고 가정한다. 모두 연결되지 않고 각각 자기 자신만을 요소로 갖고 있을 때, 아래표와 같이 표현할 수 있다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 부모 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
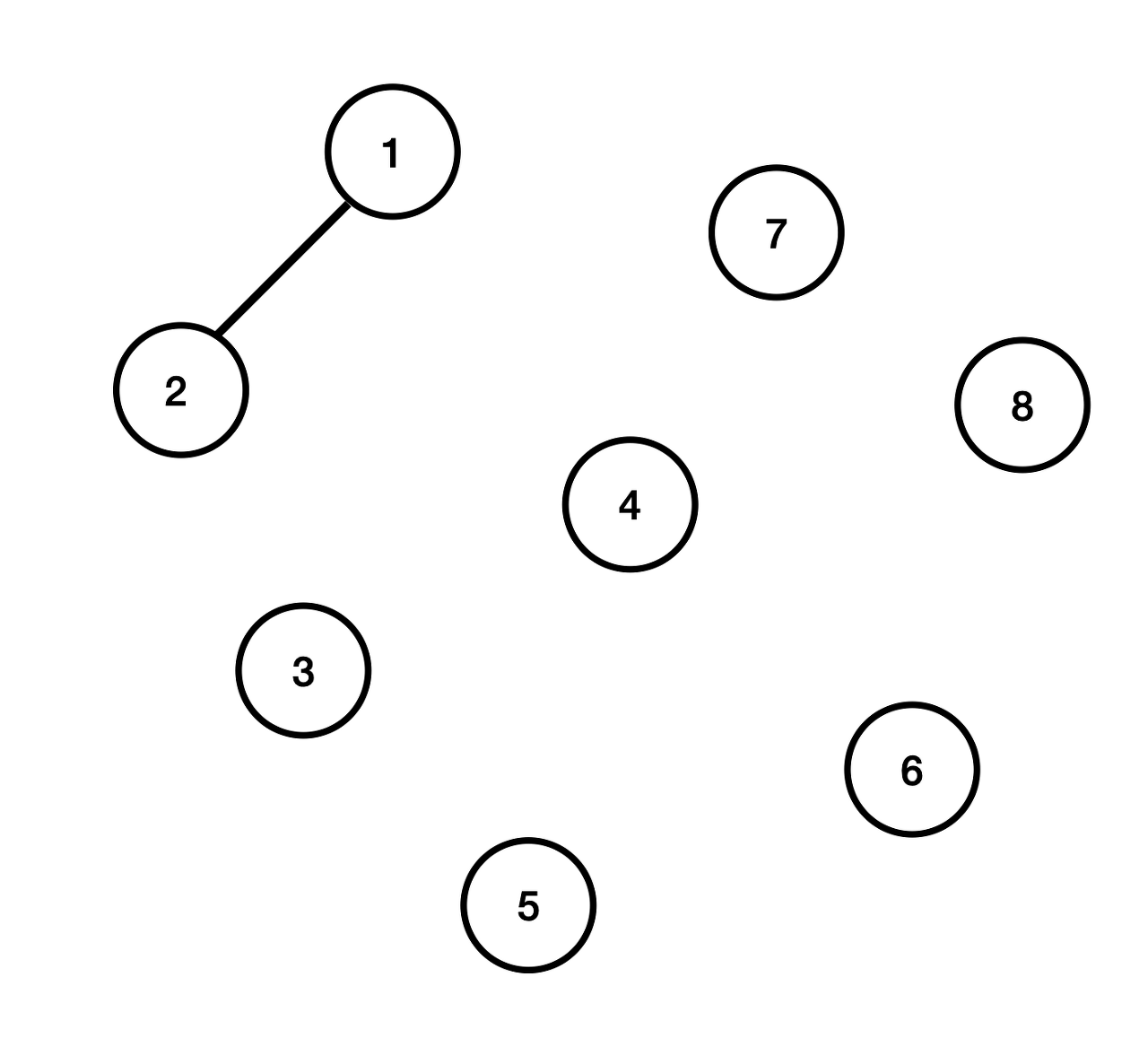
1번 노드와 2번 노드가 연결되면 2번 노드의 부모 노드 번호(인덱스)에는 "1"이 할당되고, 아래표처럼 표현할 수 있다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 부모 노드 번호 | 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 |
부모 노드를 합칠 때는 일반적으로 더 작은 값으로 이것을 Union이라고 부른다.
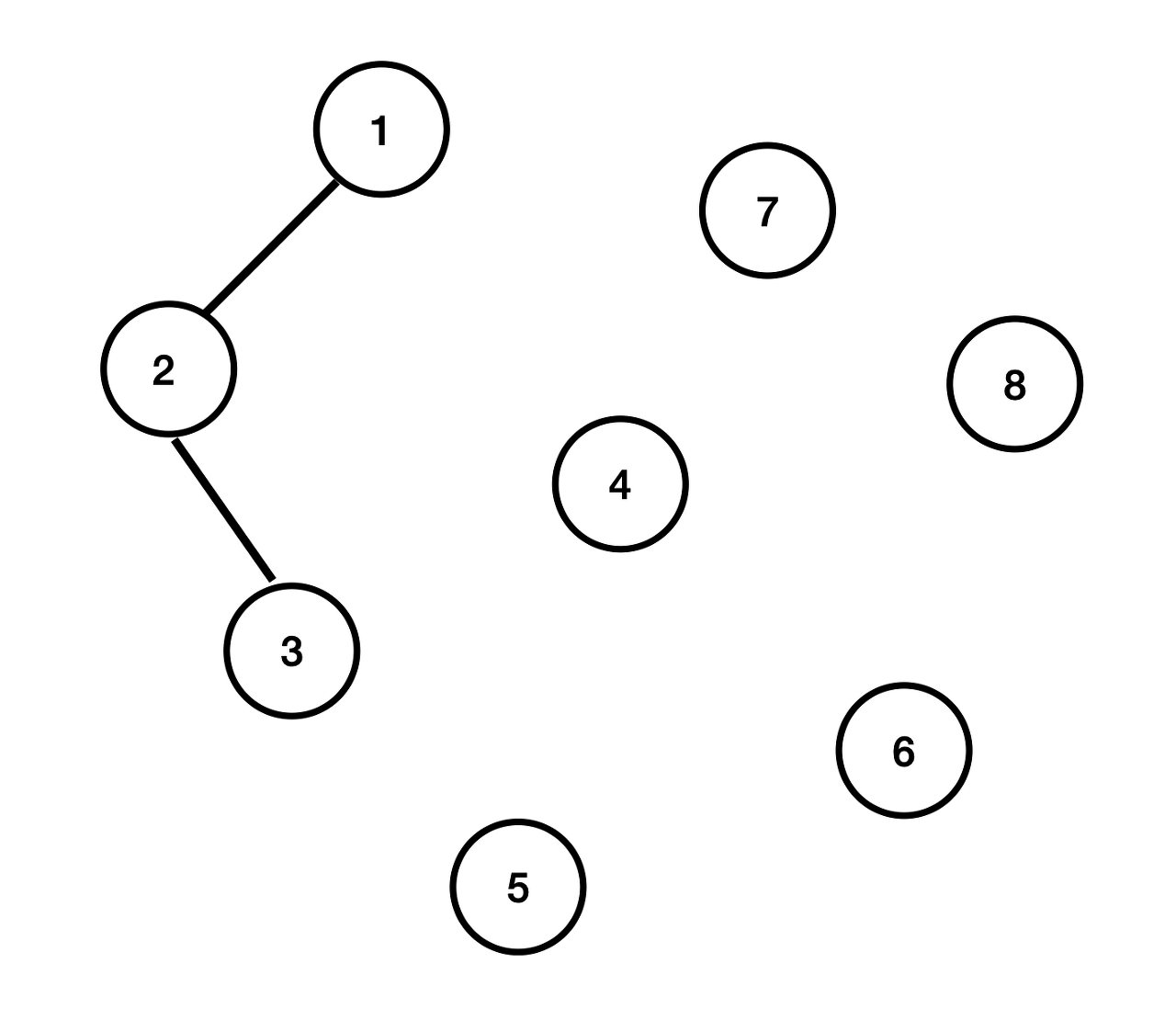
2번 노드와 3번 노드가 연결되면 마찬가지로 3번 노드의 부모 노드 번호(인덱스)에는 "2"가 할당되고, 아래 표처럼 표현할 수 있다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 부모 노드 번호 | 1 | 1 | 2 | 4 | 5 | 6 | 7 | 8 |
하지만 1번 노드와 3번 노드가 연결되었는지 확인 작업이 필요하다. 3번 노드의 현재 부모 노드로 할당된 2번 노드를 찾고, 그 다음 2번 노드의 부모 노드인 1번 노드를 찾아 3번 노드는 1번 노드까지 연결되어있다는 사실을 파악할 수 있다. 이는 재귀 함수를 통해 확인할 수 있다.

위 그래프는 아래표와 같이 나타낼 수 있다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 부모 노드 번호 | 1 | 1 | 1 | 4 | 4 | 4 | 7 | 7 |
Ex) 함수
/**
* 대표적인 그래프 알고리즘 Union-Find (합집합 찾기)
* 여러개의 노드가 존재할때 두 개의 노드를 선택해서 같은 그래프에 속하는지 판별하는 알고리즘
*/
function solution() {
/*
배열의 인덱스는 노드 번호를 뜻하고
배열의 인덱스의 값은 부모 노드를 의미한다.
최초 배열에는 자기 자신이 부모 노드로 존재한다.
예시) 입력 n = 3 -> [empty, 1, 2, 3] 배열 생성
노드 1의 부모 노드: 1,
노드 2의 부모 노드: 2,
노드 3의 부모 노드: 3
*/
const arr = [];
for (let i = 1; i <= 10; i++) arr[i] = i;
// 간선 연결
unionParent(arr, 1, 2);
unionParent(arr, 2, 3);
unionParent(arr, 3, 4);
unionParent(arr, 5, 6);
console.log(arr);
console.log(findParent(arr, 1, 2)); // true
console.log(findParent(arr, 1, 3)); // true
console.log(findParent(arr, 1, 3)); // true
console.log(findParent(arr, 4, 5)); // false
}
// 최상위 부모 노드를 찾는 재귀함수
// : x가 어떤 집합에 속해있는지 재귀 함수를 이용해서 찾는다.
function getParent(arr, x) {
if (arr[x] === x) return x;
return arr[x] = getParent(arr, arr[x]);
}
// a와 b가 속한 집합(parent)을 찾아 둘중 더 작은 부모 값으로 병합한다.
function unionParent(arr, a, b) {
a = getParent(arr, a);
b = getParent(arr, b);
// 두 노드 중 작은 부모 노드값을 가진 값으로 합친다.
if (a < b) arr[b] = a;
else arr[a] = b;
}
// a와 b가 속한 집합(parent)이 같은 부모를 갖는지 확인한다.
function findParent(arr, a, b) {
return getParent(arr, a) === getParent(arr, b);
}Ex) 트리
각 원소가 포함된 트리의 루트를 찾은 뒤, 이들이 같은지 비교해서 두 원소가 같은 트리에 속해 있는지 확인할 수 있다. 이런 find 연산을 구현하기 위해서는 모든 자식 노드가 부모에 대한 정보를 가지고 있어야 한다. 반면, 부모는 자식으로 내려갈 필요가 없기 때문에 부모는 자식에 대한 정보를 가지고 있을 필요가 없다. 루트는 부모가 없기 떄문에 보통 자기 자신을 가리키게 구현한다.
트리로 집합 표현을 하면 union 연산이 굉장히 쉽다. 각 트리의 루트를 찾은 뒤, 하나를 다른 한쪽의 자손으로 넣어주면 된다.
class NaiveDisjointSet {
/**
* @param {number} n The number of elements
*/
constructor(n) {
this.parent = new Array(n).fill(0).map((_, i) => i);
}
/**
* @param u
* @return {number} The root node
*/
find(u) {
if (u === this.parent[u]) return u;
return this.find(this.parent[u]);
}
/**
* @param {number} u Element 1
* @param {number} v Element 2
*/
merge(u, v) {
let u_root = this.find(u);
let v_root = this.find(v);
if (u_root === v_root) return;
this.parent[u] = v;
}
}최적화하기
트리를 사용하면 연산의 순서에 따라 잘못하면 트리가 한쪽에 치우쳐질 수 있다는 문제를 피할 수 없다. 이 문제를 해결하기 위해 트리를 합칠 때 항상 '높이가 더 낮은 트리'를 '높이가 더 높은 트리' 밑에 집어넣음으로써 트리가 치우쳐지는 상황을 방지한다. 이 최적화를 랭크에 의한 합치기(union-by-rank) 최적화라고 한다.
class DisjointSet {
/**
* @param {number} n The number of elements
*/
constructor(n) {
this.parent = new Array(n).fill(0).map((_, i) => i);
this.rank = new Array(n).fill(1); // 노드가 한 트리의 루트인 경우 해당 트리의 높이를 저장한다.
}
/**
* @param u
* @return {number} The root node
*/
find(u) {
if (u === this.parent[u]) return u;
// parent[u]를 루트로 바꿔 다음번에 find(u)가 호출됐을 때는 경로를 따라 찾아 올라갈 필요가 없어지게 한다(경로 압축; path compression).
return this.parent[u] = this.find(this.parent[u]);
}
/**
* @param {number} u Element 1
* @param {number} v Element 2
*/
merge(u, v) {
let u_root = this.find(u);
let v_root = this.find(v);
if (u_root === v_root) return;
if (this.rank[u_root] > this.rank[v_root]) [this.rank[u_root], this.rank[v_root]] = [this.rank[v_root], this.rank[u_root]];
// 이제 rank[v_root]가 항상 rank[u_root] 이상이므로 u_root를 v_root의 자식으로 넣는다.
this.parent[u_root] = v_root;
if (this.rank[u_root] === this.rank[v_root]) this.rank[v_root]++;
}
}이렇게 최적화를 마친 DisjointSet은 찾기와 합치기 연산을 아주 많이 수행했을 때, 각 수행에 대해 상수 시간에 동작한다. 구현이 간단하고 동작 속도가 아주 빠르기 때문에 다른 알고리즘의 일부(대표적으로 Kruscal)로 사용되는 경우가 많다.
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] 완전 탐색과 종류 (Brute Force Search) (1) | 2023.03.20 |
|---|---|
| [Algorithm] Tail Recursion (꼬리 재귀) (0) | 2023.03.19 |
| [Algorithm] DFS (깊이 우선 탐색. Depth-first search) (1) | 2023.03.13 |
| [Algorithm] 완전 탐색 - 백트래킹(Backtracking), 깊이 우선 탐색(DFS. Depth-first search) (0) | 2023.03.13 |
| [Algorithm] BFS (너비 우선 탐색. Breadth-first search) (0) | 2023.03.13 |


댓글