Graph(그래프)
- 객체 간의 연결을 시각화한 것으로 정점(Vertex)간의 관계를 표현하는 자료구조
- 단순히 노드(N, node)와 그 노드를 연결한 간선을 하나로 모아놓은 자료 구조. 즉, 연결되어 있는 객체간의 관계를 표현할 수 있는 자료구조이다.
- nodes/vertices(노드) 사이에 edge(엣지)가 있는 collection
- directed(방향) 그래프는 일방통행
- undirected(무방향) 그래프는 양방향
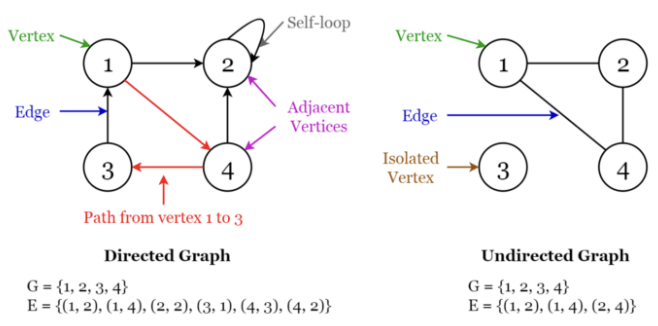
→ 소셜 미디어 네트워크를 나타내는 데 사용
→ 검색 엔진에 의해 웹 페이지 및 링크를 나타내는 데 사용
→ GPS에서 위치와 경로를 나타내는 데 사용
그래프의 용어
- 정점(vertex) : 그래프를 형성하는 노드
- 간선(edge) : 그래프에서 노드 간의 연결 (정점 간에 '선') - 아크라고도 함
- 정점 차수(degree of vertex) : 해당 정점에 연결된 간선의 개수
- 인접 노드 : 간선에 의해 직접 연결된 노드
- 완전 그래프 : 모든 정점이 간선으로 연결된 그래프. 그리고 그래프의 부분집합을 부분 그래프라고 한다.
- 희소 그래프(sparse graph) : 정점들 간에 가능한 연결 중 일부만 존재하는 경우 해당 그래프를 희소 그래프라고 한다.
- 밀집 그래프(dense graph) : 다양한 정점들 간에 연결이 많은 경우 해당 그래프를 밀집 그래프라고 한다.
- 순환 그래프(cyclical graph) : 어떤 정점에서 출발해 해당 정점으로 다시 돌아오는경로가 존재하는 지향성 그래프
- 가중치(weight) : 간선에 대한 값. 문맥에 따라 다양한 것을 나타낼 수 있음.
무방향 그래프/방향 그래프
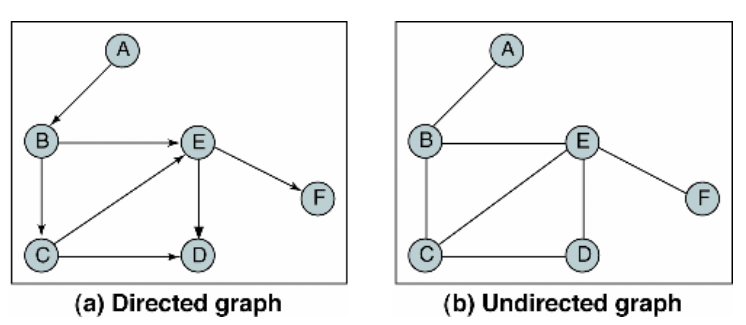
무방향 그래프: 간선 간에 방향이 없는 그래프. 간선은 두 노드 간에 방향 없이 상호 연결을 암시한다
방향 그래프 : 간선 간에 방향이 있는 그래프
그래프를 자료구조로 표현하는 방법

① 인접 행렬(adjacency matrix) : 행렬의 각 항목이 두 정점간의 연결을 나타내는 VxV 행렬임
장점
- 구현하기 간단
- 정점 간의 연결여부 확인시 O(1) 시간 요구됨
단점
- 간선의 수와 무관하게 항상 n^2개의 메모리 공간 필요
- 특정 노드의 인접 노드를 탐색하기 위해서는 모든 노드를 확인해야 함

② 인접 리스트(adjacency list) : 정점을 노드의 키로 사용하며 해당 노드의 이웃들을 리스트에 저장한다.
- 그래프 내에 적은 숫자의 간선을 가지는 경우에 용이
- 배열이나 연결 리스트로 구현이 가능
장점
- 연결된 간선의 정보만을 저장하여 O(E)의 공간만을 필요로 하므로 공간 효율성 우수(E=edge,간선)
단점
- 각 정점간의 연결여부 확인을 위해서 O(v)의 시간 복잡도를 가짐(v= vertex,정점)
무방향 그래프 / 방향 그래프 구현
1. 무방향 그래프
class UndirectedGraph {
constructor() {
this.edges = {};
}
// 정점 추가하기
addVertex(vertex) {
this.edges[vertex] = {}; // 객체에서 []를 쓰면 그게 키(key)라는 얘기
}
// 간선 추가하기
addEdge(vertex1, vertex2, weight) {
if (weight === undefined) {
weight = 0;
}
this.edges[vertex1][vertex2] = weight;
this.edges[vertex2][vertex1] = weight;
}
// 간선 삭제하기
removeEdge(vertex1, vertex2) {
if (this.edges[vertex1] && this.edges[vertex1][vertex2] !== undefined) {
delete this.edges[vertex1][vertex2];
}
if (this.edges[vertex2] && this.edges[vertex2][vertex1] !== undefined) {
delete this.edges[vertex2][vertex1];
}
}
// 정점 삭제하기
// (하나의 정점이 삭제될 때는 그 정점과 연결된 간선이 삭제되니까 상대편 정점에서도 그 간선을 지워줘야 한다.)
removeVertex(vertex) {
for (let adjacentVertex in this.edges[vertex]) {
this.removeEdge(adjacentVertex, vertex);
}
delete this.edges[vertex];
}
}
const graph1 = new UndirectedGraph();
graph1.addVertex(1);
graph1.addVertex(2);
graph1.addVertex(3);
graph1.addVertex(4);
graph1.addVertex(5);
graph1.addEdge(1, 2, 1);
graph1.addEdge(1, 5, 88);
graph1.addEdge(2, 3, 8);
graph1.addEdge(3, 4, 10);
graph1.addEdge(4, 5, 100);
console.log(graph1.edges);
const graph2 = new UndirectedGraph();
graph2.addVertex(1);
graph2.addVertex(2);
graph2.addVertex(3);
graph2.addVertex(4);
graph2.addVertex(5);
graph2.addEdge(1, 2, 1);
graph2.addEdge(1, 5, 88);
graph2.addEdge(2, 3, 8);
graph2.addEdge(3, 4, 10);
graph2.addEdge(4, 5, 100);
graph2.removeVertex(5);
graph2.removeVertex(1);
graph2.removeEdge(2, 3);
console.log(graph2.edges);
graph1은 위의 그림을 나타낸다.
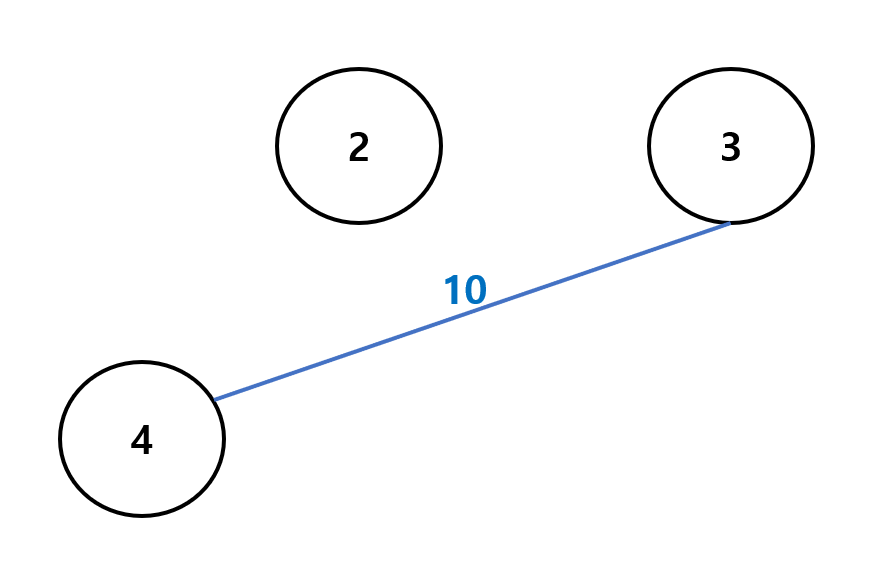
graph2는 graph1에서 1번과 5번 정점을 삭제하고 2번과 3번 사이의 간선을 삭제한 위의 그림을 나타낸다.
2. 방향 그래프
class DirectedGraph {
constructor() {
this.edges = {};
}
//정점을 추가하는 함수
addVertex(vertex) {
this.edges[vertex] = {};
}
//간선을 추가하는 함수
addEdge(originVertex, destVertex, weight) {
// 시작 정점, 도착 정점, 가중치
if (weight === undefined) {
weight = 0;
}
this.edges[originVertex][destVertex] = weight;
}
}
const graph1 = new DirectedGraph();
graph1.addVertex("A");
graph1.addVertex("B");
graph1.addVertex("C");
graph1.addEdge("A", "B", 1);
graph1.addEdge("B", "C", 2);
graph1.addEdge("C", "A", 3);
console.log(graph1.edges);
graph1은 위의 그림을 나타낸다.
트리와의 차이점
사실 트리도 그래프의 한 종류이다.
(트리는 하나의 부모노드에서부터 아래 방향으로 내려오는 방향이 있다. 그러나 트리는 항상 그 방향이니까 표시를 하지 않은 것 뿐임. 루트가 있고 In-degree가 1인 방향 그래프)

'[Basic] Data > Data Structure' 카테고리의 다른 글
| [Data Structure] 비선형 - Heap(힙) (0) | 2023.02.21 |
|---|---|
| [Data Structure] 비선형 - Tree(트리) (0) | 2023.02.21 |
| [Data Structure] 비선형 - Hash Table(해시 테이블) (0) | 2023.02.21 |
| [Data Structure] 선형 - Queue(큐) (0) | 2023.02.21 |
| [Data Structure] 선형 - Stack(스택) (0) | 2023.02.21 |




댓글