LIS (Longest Increasing Sebsequence)
최장 증가수열 문제는 어떤 배열에서 특정 부분을 지워 만들 수 있는 증가 부분수열 중 가장 긴 수열을 구하는 문제다.
배열이 [1, 4, 4, 6, 8, 3]이면 증가부분수열은 [1, 4, 6, 8], [4, 6, 8], [4, 8], [6, 8]이다. 여기서 가장 긴 증가 부분수열은 [1, 4, 6, 8]이다.가장 쉬운 방법은 모든 증가부분수열을 구해 가장 긴 것을 찾는 것이지만, 같은 연산을 반복하기 때문에 O(2^n)의 시간복잡도를 가진다. 이 문제를 효율적으로 해결하는 두 가지 방법이 있다.
Ex)

배열 (1, 5, 4, 2, 3, 8, 6, 7, 9, 3, 4, 5) 에서 부분 수열 (1, 2, 3, 6, 7, 9) 는 전체 수열 중, 오름차순으로 증가하는 가장 긴 부분 수열이다.
주어진 수열에서 LIS의 길이를 구하는 두 가지 방법을 알아보자.
동적 계획법 : O(N^2)
최장 증가 수열을 찾는 가장 단순한 방법은 완전 탐색일 것이다. 하지만 수열에 존재하는 수의 개수가 k개일 때, 1개 이상의 원소를 갖는 모든 부분수열의 가짓수는 2^k개이므로, 모든 부분수열을 확인해 이들이 오름차순으로 정렬되어 있는지 확인하는 것은 매우 비효율적이다. 따라서 다이나믹 프로그래밍을 통해 이를 구현할 수 있다.

수열의 한 원소에 대해, 그 원소에서 끝나는 최장 증가 수열을 생각해보자. 그 최장 증가 수열의 k를 제외한 모든 원소들은 반드시 k보다 작아야 할 것이다. 따라서 k의 앞 순서에 있는 모든 원소들 중 값이 k보다 작은 원소에 대해, 그 각각의 원소에서 끝나는 최장 증가 수열의 길이를 알고 있다면, k에서 끝나는 최장 증가 수열의 길이도 구할 수 있을 것이다.
위의 예시에서는 8 이전의 (1, 5, 4, 2, 3)까지의 수열 중 각각의 원소에서 끝나는 최장 증가 수열의 길이는 다음과 같다.
- 1에서 끝나는 LIS 길이 : 1 (1)
- 5에서 끝나는 LIS 길이 : 2 (1, 5)
- 4에서 끝나는 LIS 길이 : 2 (1, 4)
- 2에서 끝나는 LIS 길이 : 2 (1, 2)
- 3에서 끝나는 LIS 길이 : 3 (1, 2, 3)
이들 중 가장 긴 (1, 2, 3)에 현재 수 8을 더한 (1, 2, 3, 8)이 8에서 끝나는 최장 증가 수열이 된다.
즉, 앞 순서의 모든 원소에서 끝나는 최장 증가 수열들의 길이 중 가장 긴 것을 골라 1을 더한 것이 곧 현재 수에서 끝나는 최장 증가 수열의 길이이다.
따라서 dp[i] = "i번째 인덱스에서 끝나는 최장 증가 수열의 길이"로 정의한다.
function LIS_DP() {
for (let i = 0; i < n; ++i) {
dp[i] = 1; // 해당 원소에서 끝나는 LIS 길이의 최솟값. 즉, 자기 자신
for (let j = 0; j < i; j++) {
// i번째 이전의 모든 원소에 대해, 그 원소에서 끝나는 LIS의 길이를 확인한다.
if (arr[i] > arr[j) {
// 단, 이는 현재 수가 그 원소보다 클 때만 확인한다.
dp[i] = Math.max(dp[i], dp[j] + 1); // dp[j] + 1 : 이전 원소에서 끝나는 LIS에 현재 수를 붙인 새 LIS 길이
}
}
}
}이분 탐색을 이용한 방법 : O(NlogN)
DP를 이용한 방법은 분명 완전 탐색에 비해 시간 복잡도 면에서 효율적이지만, 여전히 O(N^2)이라는 점이 발목을 잡는다.
이 때, 이분 탐색(Binary Search)을 사용하면 시간 복잡도를 O(NlogN)으로 줄일 수 있다.
이 방법에서는 LIS를 기록하는 배열을 하나 더 두고, 원래 수열에서의 각 원소에 대해 LIS 배열 내에서의 위치를 찾는다.
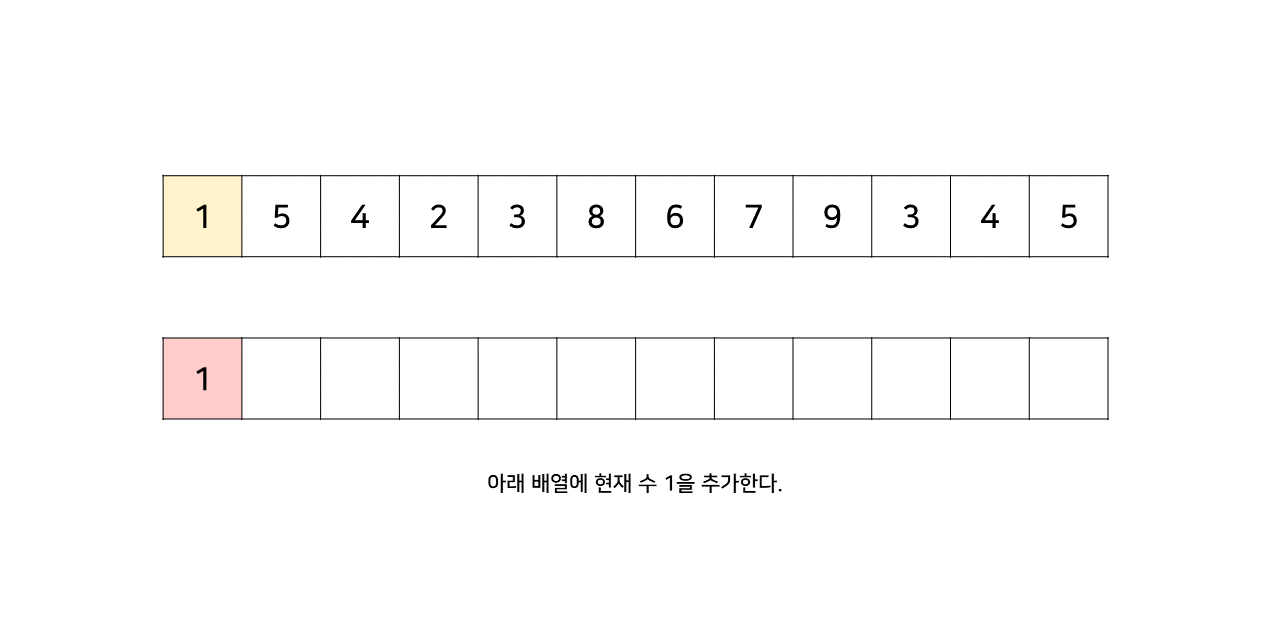



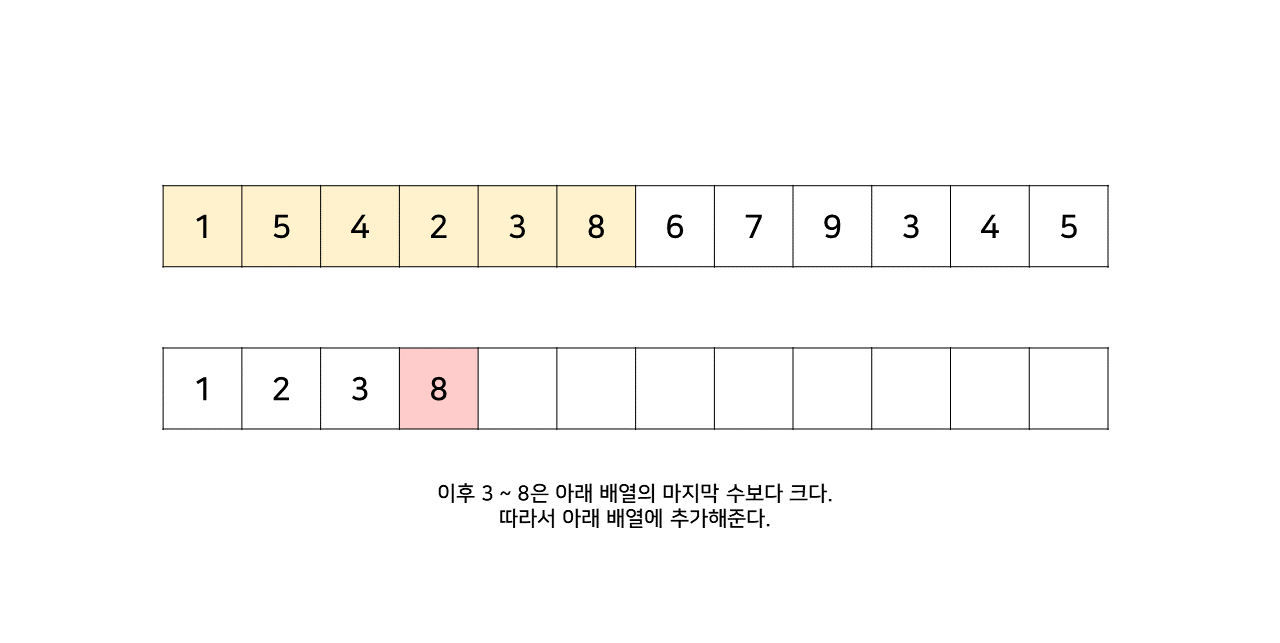

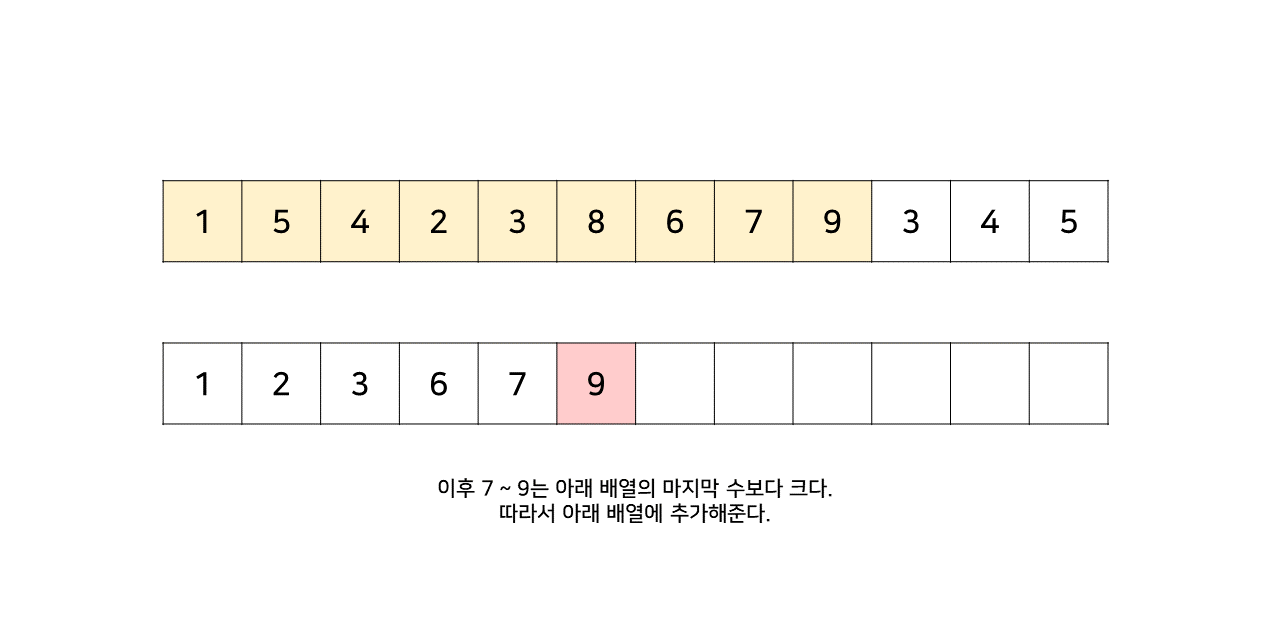


그림의 아래 배열의 크기는 최대 6까지 갔었으므로, LIS의 길이는 6이 된다.
이 방법은 그림의 아래 배열을 LIS의 형태로 유지하기 위해, 기존 수열의 각 원소가 LIS에 들어갈 위치를 찾는 원리로 동작한다.
즉, 현재 원소를 아래 배열에 넣어 LIS를 유지하려고 할 때, 그 최적의 위치를 찾는 것이다.
const arr = [1, 5, 4, 2, 3, 8, 6, 7, 9, 3, 4, 5];
function binary_search(lis, start, end, element) {
// 이분 탐색으로 lis 내에서 element의 위치를 반환
// lis의 start - end 구간에서만 확인
while (start < end) {
const mid = Math.floor((start + end) / 2);
if (element > lis[mid]) start = mid + 1;
else end = mid;
}
return end;
}
function LIS_BS() {
let ret = 0;
const lis = [];
lis.push(arr[0]);
for (let i = 1; i < n; i++) {
// 만약 lis의 마지막 수보다 i번째 수가 크다면, 그냥 뒤에 붙인다.
if (arr[i] > lis.at(-1)) {
lis.push(arr[i]);
ret = lis.length() - 1;
}
// i번째 수에 대해, lis 내에서 그 수의 위치를 찾는다.
let pos = binary_search(lis, 0, ret, arr[i]);
lis[pos] = arr[i];
}
return ret + 1;
}이분 탐색 정리
이분 탐색을 사용한 아이디어는 정리하면 다음과 같다.
LIS를 만드는 과정을 보면 LIS의 마지막 원소가 가능한 작을수록 더 긴 LIS를 생성할 수 있다는 것을 알 수 있다. 따라서 현재 생성된 LIS가 있는데 새로운 원소가 LIS의 마지막 원소보다 작은 경우, 들어갈 위치를 이분 탐색으로 찾은 후 대체시키며 LIS를 찾을 수 있다.
예를 들어 배열이 [1, 2, 3, 7, 5, 6]일 때 5까지 탐색한 경우, 가능한 LIS는 [1, 2, 3, 7]과 [1, 2, 3, 5]다. 하지만 더 긴 LIS를 만들기 위해서는 [1, 2, 3, 5]가 더 유리하다.
따라서 [1, 2, 3, 7] 다음 5가 들어온다면 7과 바꿔주는 것이다.
const arr = [1, 2, 3, 7, 5, 6];
const lis = [];
lis.push(arr[0]);
for (let i = 1; i < arr.length; i++) {
// 이분 탐색으로 위치 찾기
let left = 0, right = lis.length;
while (left < right) {
const mid = Math.floor((left + right) / 2);
if (arr[i] > lis[mid]) left = mid + 1;
else right = mid;
}
if (right === lis.length) lis.push(arr[i]);
else lis[right] = arr[i];
}각 원소에 대해 이분 탐색으로 확인하기 때문에 의 시간복잡도를 가진다.
주의해야할 점은 lis 배열의 원소가 최장증가수열과 일치하지 않는다는 것이다. 오직 길이만을 알 수 있다.
최장증가수열을 알고싶다면 배열을 하나둬서 각 원소가 들어간 인덱스를 저장하면 된다. 이 배열을 사용해서 동적 계획법에서 한 것처럼 거꾸로 이어나가면 된다.
'[Basic] Data > Algorithm' 카테고리의 다른 글
| [Algorithm] 동적 계획법 (DP. Dynamic Programming) (0) | 2023.03.13 |
|---|---|
| [Algorithm] 최소 공통 조상 (LCA. Lowest Common Ancestor) (0) | 2023.03.13 |
| [Algorithm] 선형 탐색, 분할 정복, 이진 탐색(Binary Search) (0) | 2023.03.09 |
| [Algorithm] 계수 정렬 (Counting Sort) (1) | 2023.03.08 |
| [Algorithm] 힙 정렬 (Heap Sort) (0) | 2023.02.27 |




댓글