Kruskal · developeSHG/Data_Structure-Algorithm@e91776c
developeSHG committed Aug 17, 2023
github.com
다시 복습하면 그래프는 [현실 세계의 사물이나 추상적인 개념간]의 [연결 관계]를 표현한다 했었다.
전형적인 그래프는 정점들과 정점들을 연결하는 간선으로 이루어진 것이 그래프였고, 예로 소셜 네트워크 관계도, 지하철 노선도를 그래프로 표현할 수 있었다.
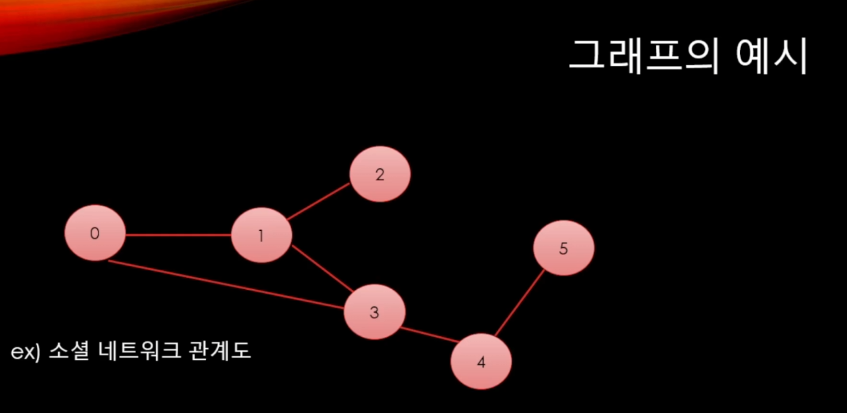
위 사진처럼 정점에 대한 간선을 연결해서 모든 길을 뚫어놓은 상태이고, BFS나 DFS 등 다양한 알고리즘을 적용시켜 분석했지만, 이제는 거꾸로 스패닝 트리는 길을 연결하는 과정부터 생각해본다.

이게 무슨 말이냐면, 각 정점들마다 길이 있는데 이 길중에서 스패닝 트리란 것은 간선을 최소화 해서 모든 정점을 연결하는 것을 말한다.
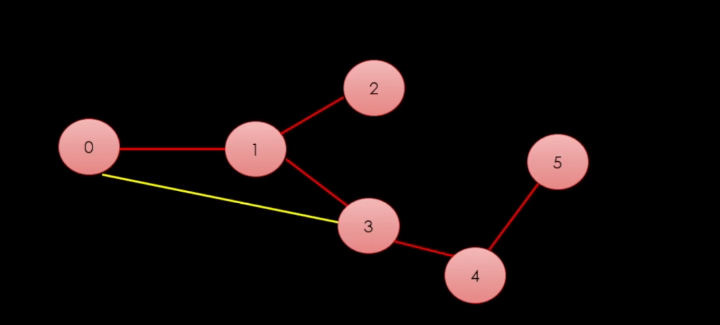
이렇게 빨간 간선으로만 연결했을 경우, 간선이 최소화가 된다.
간선을 최소화 한다는 말은 "사이클"이 생기면 안된다는 말이다. 사이클이 생길 경우, 스패닝 트리로 인정할 수 없다.
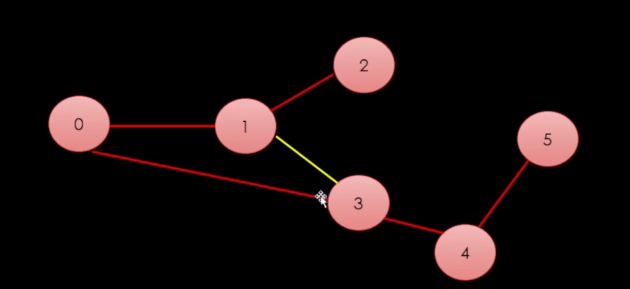
이것도 스패닝 트리라고도 볼 수 있다. (여러가지가 존재함)
N개의 정점이 있을 경우 N-1개의 간선으로 연결이 가능하다.

예시

중요한 것은 모든 정점이 연결되어 있을 필요는 없지만, 하나라도 정점이 순환(사이클)이 되면 안되 하나의 정점에서 다른 정점으로 갈 수 있는 경로가 간접적이건 직접적이건 확보가 되어있어야 한다.
최소 스패닝 트리 (MST)
이전에 그래프를 학습했을 때도, 그래프마다 가중치를 기준으로 다익스트라 알고리즘을 적용시켜 최단 거리를 구할 수 있었다.
이번에도 전과 동일하게 스패닝 트리를 곧이 곧대로 만드는 것이 아니라, 모든 경로의 합이 최소가 되는 것을 구하는 것이 최소 스패닝 트리다.
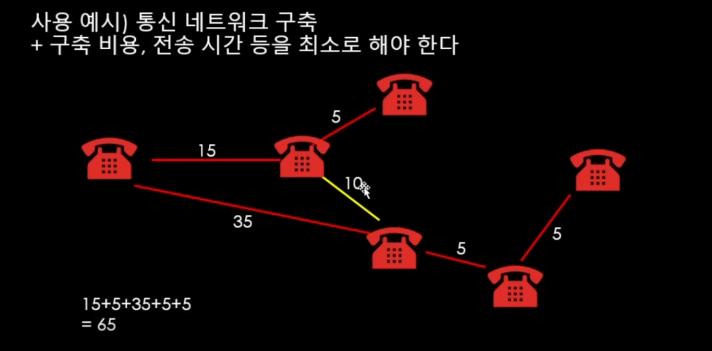
어떤 간선으로 연결을 해야 가중치가 가장 작은지 봐야한다.

크루스칼 (KRUSKAL) MST 알고리즘

이 상황에 대해서 길을 선택해 만들었을 때 => 최소 스패닝 트리를 만들어 줘야 할 경우.
가장 대표적인 알고리즘들 중에 대표적인 애가 Kruskal 알고리즘이 있다. (직관적이고 단순한 형태이기 때문)
Kruskal은 탐욕적인(greedy) 방법을 이용을 한다.
=> 지금 이순간에 최적인 답을 선택하여 결과를 도출하는 방법이다.
직관을 사용하는 것 처럼 모든 경로를 다 본다음에 가장 작은 부분부터 본다.
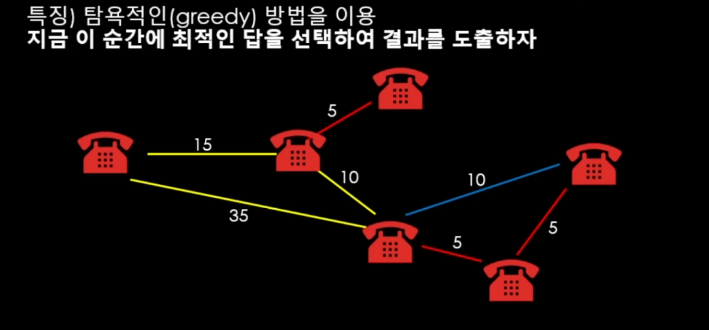
그리디. 즉 탐욕적인 방식인 만큼 가중치가 적은 순대로 연결하니 5부터 순서대로 연결해주면 된다는 원리가 된다.
하지만 중간에 사이클이 발생하는지 안하는지도 이중으로 확인을 해야한다 => (5가 연결된 상태에서 파란색 선 10을 연결하면 사이클이 발생한다. 규칙 위반)
기본적으로 작은 가중치순으로 연결하는 건 맞되, 이중으로 체크해서 사이클이 발생하지 않는지 길을 만들어야 한다는 게 핵심이다.
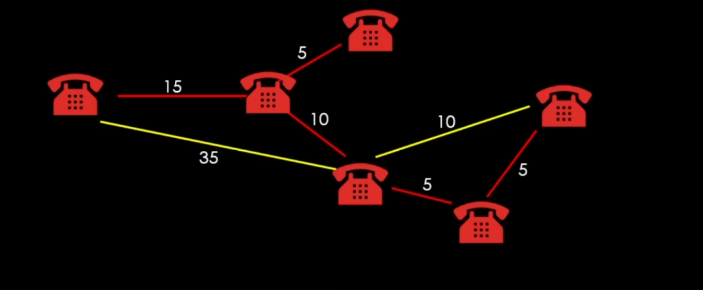
이렇게 연결이 된다.
문제 - 사이클이 생길 수 있는 상황을 어떻게 판별할까?
그래프에서 실시간으로 사이클이 생기는지 판별할 수 있겠지만, 너무 복잡하고 단순하게 모든 단위를 다 "그룹"단위로 관리를 하는 것이다.
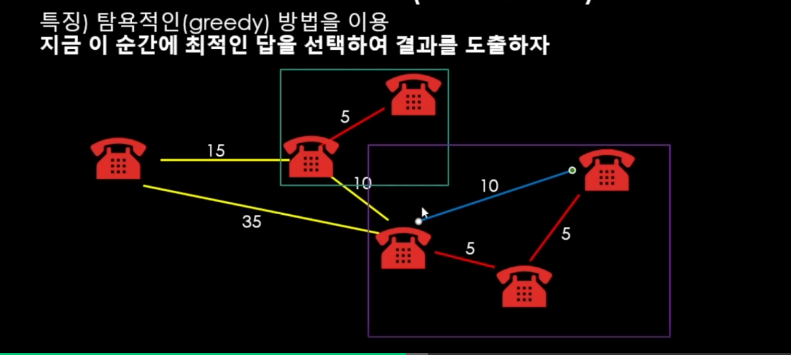
즉, 각기 다른 그룹 끼리만 연결할 수 있다는 규칙으로 관리하면 된다.
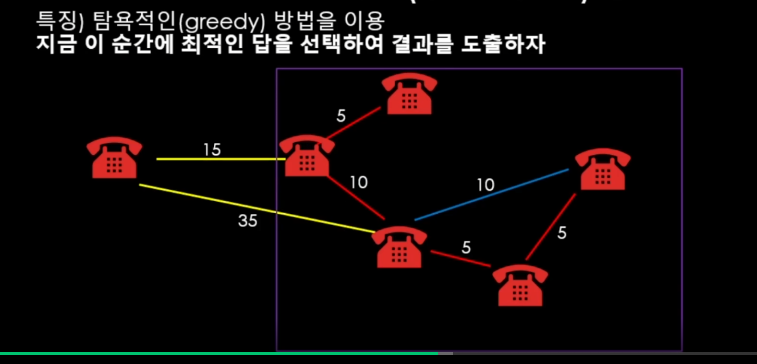
이런 식으로 그룹이 합쳐질 것이고, 결과를 코드로 구현해야한다 치면 정점을 각 몇 번째 그룹인지 관리하고 연결하는 형태로 구현하게 될 것이다. 기존 속해있던 그룹의 정점을 하나씩 스캔하면서 연결해도 안될 것은 없지만, 바로 이전 글에서 학습했던 상호 베타적 집합(Disjoint Set)을 통해 효율적으로 관리할 수 있는 방법이 떠오른다. union-find 자료구조를 이용하게 되면 그룹핑을 해서 동일한 그룹을 병합할 수 있는 손쉽게 관리할 수 있다.
Krulskal 알고리즘은 MST를 만들어주는 "알고리즘" 정도라고 생각하면 된다.
그리고 A*의 우선순위 큐를 도구로 활용하는 것처럼, Kruskal 알고리즘을 구현하면서 도구처럼 사용하면 좋은게 DSU(Disjoint Set)
다.
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
using namespace std;
#include <thread>
// 그래프/트리 응용
// 오늘의 주제 : 최소 스패닝 트리 (Minimum Spanning Tree)
class DisjointSet
{
public:
DisjointSet(int n) : _parent(n), _rank(n, 1)
{
for (int i = 0; i < n; i++)
_parent[i] = i;
}
// 조직 폭력배 구조?
// [1] [3]
// [2] [4][5][0]
//
// 니 대장이 누구니?
int Find(int u)
{
if (u == _parent[u])
return u;
//_parent[u] = Find(_parent[u]);
//return _parent[u];
return _parent[u] = Find(_parent[u]);
}
// u와 v를 합친다
void Merge(int u, int v)
{
u = Find(u);
v = Find(v);
if (u == v)
return;
if (_rank[u] > _rank[v])
swap(u, v);
// rank[u] <= rank[v] 보장됨
_parent[u] = v;
if (_rank[u] == _rank[v])
_rank[v]++;
}
private:
vector<int> _parent;
vector<int> _rank;
};
struct Vertex
{
// int data;
};
vector<Vertex> vertices;
vector<vector<int>> adjacent; // 인접 행렬
void CreateGraph()
{
vertices.resize(6);
adjacent = vector<vector<int>>(6, vector<int>(6, -1));
adjacent[0][1] = adjacent[1][0] = 15;
adjacent[0][3] = adjacent[3][0] = 35;
adjacent[1][2] = adjacent[2][1] = 5;
adjacent[1][3] = adjacent[3][1] = 10;
adjacent[3][4] = adjacent[4][3] = 5;
adjacent[3][5] = adjacent[5][3] = 10;
adjacent[5][4] = adjacent[4][5] = 5;
}
struct CostEdge
{
int cost;
int u;
int v;
bool operator<(CostEdge& other)
{
return cost < other.cost;
}
};
int Kruskal(vector<CostEdge>& selected)
{
int ret = 0;
selected.clear();
vector<CostEdge> edges;
for (int u = 0; u < adjacent.size(); u++)
{
for (int v = 0; v < adjacent[u].size(); v++)
{
// edge를 중복되게 넣지않기 위해 비교해서 걸러줌. (1, 2), (2, 1)
if (u > v)
continue;
int cost = adjacent[u][v];
if (cost == -1)
continue;
edges.push_back(CostEdge{ cost, u, v });
}
}
std::sort(edges.begin(), edges.end());
DisjointSet sets(vertices.size());
for (CostEdge& edge : edges)
{
// 같은 그룹이면 스킵 (안 그러면 사이클 발생)
if (sets.Find(edge.u) == sets.Find(edge.v))
continue;
// 두 그룹을 합친다
sets.Merge(edge.u, edge.v);
selected.push_back(edge);
ret += edge.cost;
}
return ret;
}
int main()
{
CreateGraph();
vector<CostEdge> selected;
int cost = Kruskal(selected);
}'[C++] Data Structure & Algorithm > MST(Minimum Spanning Tree)' 카테고리의 다른 글
| [MST] Chapter 04. Prim 알고리즘을 이용한 맵 생성 (0) | 2023.08.16 |
|---|---|
| [MST] Chapter 03. Kruskal 알고리즘을 이용한 맵 생성 (0) | 2023.08.16 |
| [MST] Chapter 01. Disjoint Set (Union-Find) (0) | 2023.08.14 |


댓글