벡터가 행렬을 갖다오게되면 변환이 된다.
사실은 우리의 좌표 자체는 위치 벡터로 관리하지만,
그 벡터가 위치가 변환하는 과정 자체는 행렬로 묘사하는 걸로 볼 수 있다.
그리고 행렬의 특징이 여러개를 준비해서 하나하나하나 거칠 필요 없이
행렬들끼리도 하나로 합쳐서 모든 동작이 한번에 일어날 수 있게 합칠 수 있다.

행렬의 정의
쉽게 생각하면 2차원 배열
안에는 스칼라 값이 들어가있다고 보면 된다.
행수와 열수
행 row. 열 col
2 x 3, 4 x 4 다양하다
[1 3]
[4 2]
에 K를 곱하면
[k 3k]
[4k 2k]
그리고 행렬의 덧셈은 포맷이 똑같아야한다
서로 2x2 라든지.
각각의 위치에 맞는 것들끼리 더해주면 된다. 단순함
사실 덧셈은 활용할 상황이 많이 없다
게임속에선 행렬의 곱을 거의 이용함
덧셈도 같은 공간끼리 더해줬던 것처럼 곱셈도 포맷이 정해져있다.

A 가 m x n
B 가 n x p
라 치면
A의 열 갯수와
B의 행 갯수가 일치해야 곱셈의 조건이 된다.
둘이 안맞으면 사이즈가 안맞아서 연산을 할 수 없다.
그럼 결과물
m x p 의 크기로 만들어 진다
행렬곱은 교환법칙이 성립하지 않는다
AB = BA 안된다.
결합법칙은 성립한다
(AB)C = A(BC)
그래서 아까말한 행렬의 동작을 한 번에 합쳐서 일어날 수 있게 가능하단말.
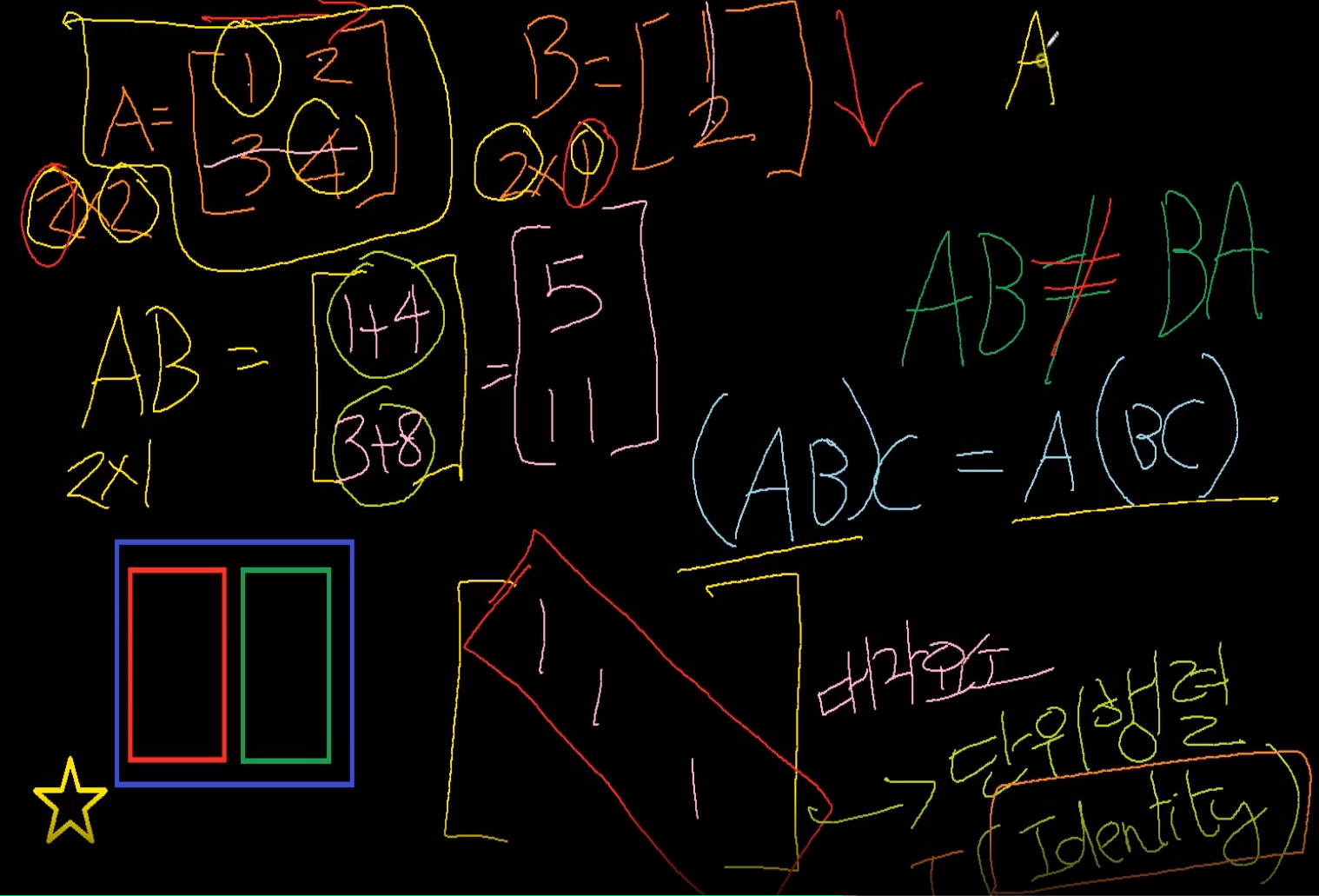
행렬의 특성
대각요소 : 1행1열, 2행2열 등 대각선에 있는 요소들
대각행렬(diagonal matrix) : 대각요소에만 값이 있고 나머지가 0으로 채워진 행렬
단위행렬(Identity) : 대각요소가 1로 채워져있고, 나머지가 0으로 채워진 행렬
단위행렬의 특징은 단위행렬에 행렬A를 곱해도 그대로 나온다
AI = A
IA = A
교환 법칙도 성립한다. (자기자신을 뱉어줌)
게임에서 사용하는 행렬은 거의 4x4 행렬을 사용한다.
왜?
행렬을 사용하는 이유는 벡터 자체를 위치 자체를 변환시키는 용도로 사용하는게 최종목적이다.
게임에선 x, y, z 에 하나를 더 둬서 v(x, y, z, 1)로 사용할 것이다.
4x4를 나오기 위해선 행과 열이 같아야 곱의 조건이 맞지만, 결과물로 나오는 열과 행도 같아야 되기 때문에
기준이 되는 행렬과 피연산자 행렬도 4x4로 크기가 동일해야한다.
행렬도 사인과 아크코사인이 있는 것처럼 역행렬이 있다.
한 방향으로 갔다가 다시 되돌리기위한 변환 행렬으로 역행렬이라 한다.
M의 역행렬 : M(-1) 상단에 지수처럼 붙는다보면 됌
항상 100%확률로 역행렬이 존재한다고 할 순없다.
0으로 다 채워진 행렬의 역행렬은 없다.
M * M(-1) = I(단위행렬)
M * M(-1) = I(단위행렬) = M(-1) * M
역행렬이 존재하는지 판단하는 법
[a b]
[c d]
의 행렬이라 하면
ad - bc 가 0이 아니면 역행렬이 있다.
D(Det) = ad - bc;
역행렬의 공식
A(-1) = (1 / Det) * [d -b]
[-c a]
[d -b]
[-c a]
의 행렬에 각각 (1 / Det)를 곱하면 역행렬이다.

전치행렬(T = Transpose)
행과 열을 뒤집은 행렬
[1 2 3] [1 4 7]
[4 5 6] = [2 5 8]
[7 8 9] [3 6 9]
특징으로는 어떤 행렬의 전치 행렬을 두번 해주면 자기 자신이 나온다.
(M(T))T = M
위 특징은 그냥 특징이고, 정작 활용이 되는 특징은 직교 행렬인 경우가 있다.
직교는 90도를 의미한다.
[0 0 1]
[1 0 0]
[0 1 0]
각 행을 벡터라 한다면 세개의 벡터는 각 좌표(x,y,z) 방향으로 크기가 1인 단위벡터다.
각 벡터끼리 내적한다면 0 이 나온다.
또한 각 벡터끼리는 직각을 이룬다. 그래서 직교행렬이라한다.
내적이 0이 나온다하면 그 두 벡터가 직각으로 이루고 있는 상황이라 한다.
위처럼 직교행렬일때의 특성은 M행렬에다 M의 전치행렬을 곱하면 단위 행렬이 나오는 큰 특성이 있다.
M * M(T) = M(T) * M = I
[0 0 1] [0 1 0] [1 0 0]
[1 0 0] * [0 0 1] = [0 1 0]
[0 1 0] [1 0 0] [0 0 1]
근데 결과가 I(단위행렬)이 되었다하는 건 역행렬인 경우인데,
이로써 알수있는건 직교행렬에 대해서는 전치행렬로 만든거 자체가 역행렬이다 라고 할 수 있다.
'DirectX 12 > Vector & Matrix' 카테고리의 다른 글
| [DirectX12 - Vector & Matrix] Chapter 06. Projection, Screen 변환 행렬 (0) | 2023.06.30 |
|---|---|
| [DirectX12 - Vector & Matrix] Chapter 05. World, View 변환 행렬 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 04. Scale, Rotation, Translation 변환 행렬 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 02. 벡터 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 01. 삼각함수 (0) | 2023.06.30 |




댓글