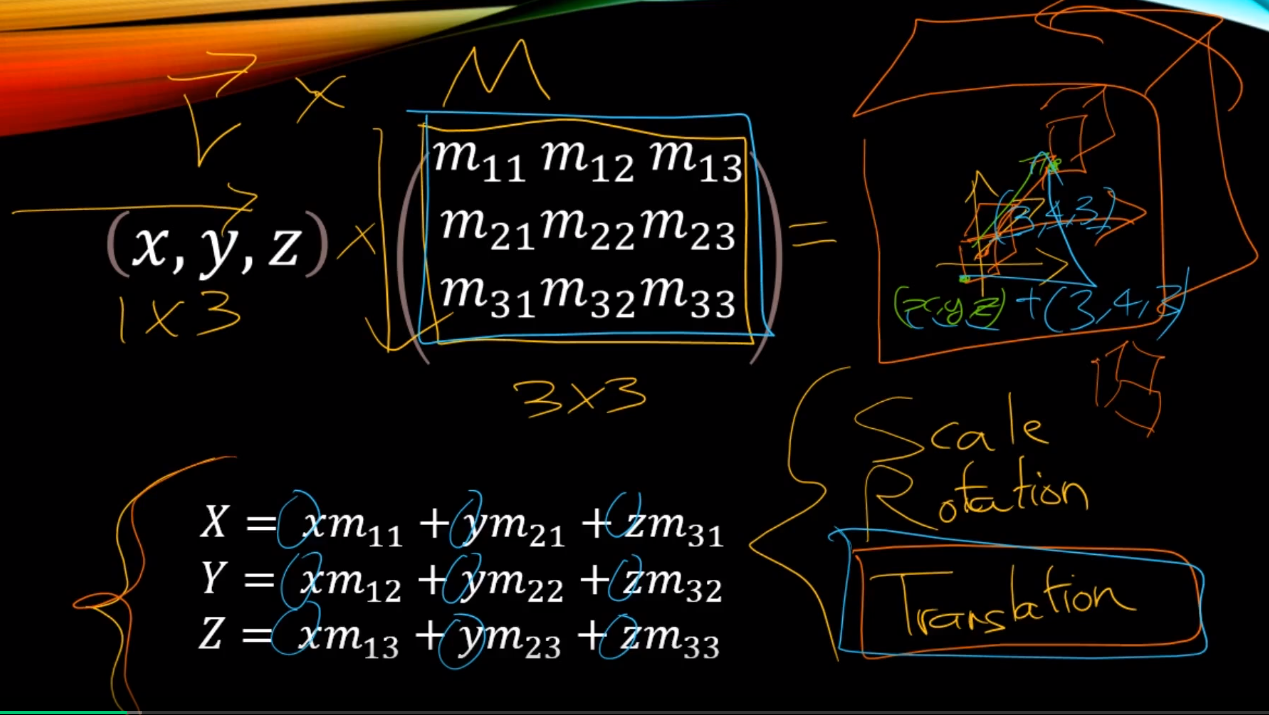
벡터를 변환시킬 떄 하는 3총사
Scale
Rotation
Translation
SRT라 함
(x, y, z) x (3x3 행렬) = 1 x 3
3d상에서 어떤 문체를 2d화면상으로 옮기는 최종적으로 투영하는 수학적으로 연산을 하게 될건데
그걸 위해서는 위에 말한 3가지처럼 다양한 연산이 필요하다.
근데 xyz 벡터에다 3x3행렬을 사용했을 때는 Translation을 표현한다고자하면
각각의 원소 계산에 x y z의 연산이 들어가기때문에 이동 변환을 할수없다.
그래서 게임에서 계산할 때는 인게임에서는 xyz 3개만을 사용하지만, 4차원으로 하나 더 만들어줘서
(x, y, z, w(1)) 로 사용한다.
이렇게 가상의 4차원 공간인것마냥 추가해줘서 사용하는 것을 동차좌표계라 한다.
w가 의미를 갖는다기보단 말그대로 연산을 도와주는 도구다. 진짜 4차원으로 사용하는것 아님.
(x, y, z 1) [m11 m12 m13 m14]
[m21 m22 m23 m24]
[m31 m32 m33 m34]
[m41 m42 m43 m44]
X = xm11 + ym21 + zm31 + m41
Y = xm12 + ym22 + zm32 + m42
Z = xm13 + ym23 + zm33 + m43
W = xm14 + ym24 + zm34 + m44

Translation 행렬의 위치
그럼 4x4 행렬에서 가장 아래에 있는
4행의 1, 2, 3열 총 3개가 x,y,z의 이동을 담당. translation 을 의미한다.
왜냐하면 마지막 행의 값들이 결과로 나오는 1x4행렬에 각각 한번씩 들어가기 때문이다.
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[a b c 0]
하지만 이렇게 하면 결과값은 이동한 좌표가 아닌 절대 좌표가 될것이다.
왜냐하면 a b c 를 제외한 다른것들이 0이기 때문에.
그럼 기존 좌표에서 새로운 이동좌표를 더할라면 대각요소를 1로 만들어야 각 x, y, z 별로 겹치지않게 기존좌표를 갖고올수있다.
그리고 결과물자체도 동차좌표계로 1로 나오길 원하므로 w 자리에는 1 그대로 갖고나와야한다.
그렇게 되면 결과물은
(x, y, z, 1) [1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[a b c 1]
X = x + a;
Y = y + b;
Z = z + c
W = 1
X = xm11(x) + ym21 + zm31 + m41(a)
Y = xm12 + ym22(y) + zm32 + m42(b)
Z = xm13 + ym23 + zm33(z) + m43(c)
W = xm14 + ym24 + zm34 + m44(1)

Scale
스케일은 기본적으로 몇배를 곱해서 커지게된다.
X = x * a;
Y = y * b;
Z = z * c
W = 1
더해주는건 아니니 Translation의 자리는 지움. 우리가 필요한건 곱하기
그리고 x는 [y,z]랑 무관. y는 [x,z]랑 무관, z는 [x,y]랑 무관
그러므로 결과물은
(x, y, z, 1) [a 0 0 0]
[0 b 0 0]
[0 0 c 0]
[0 0 0 1]
X = xm11(x * a) + ym21 + zm31 + m41
Y = xm12 + ym22(y * b) + zm32 + m42
Z = xm13 + ym23 + zm33(z * c) + m43
W = xm14 + ym24 + zm34 + m44(1)

Rotation
이건 굳이 외우지 않아도 됌


이렇게 SRT를 통해 벡터를 변환시킬 수 있다.
그리고 행렬은 합칠수있다고 했다.
하지만 순서는 지켜줘야한다.
Scale -> Rotation -> Translation
Translation은 상관없지만
ROtation의 경우 원점에서 회전하는것이기때문에 만약 R을 맨뒤로 하면 공전하는 느낌으로 회전한다.
Scale도 중점을 기준으로 위치는 변하지 않은채 커져야하기떄문이다.
Rotation을 먼저로 온다하더라도, 회전을 한채 원점에서의 scale이 커지기때문에 모양이 예상과 다르게 된다.
'DirectX 12 > Vector & Matrix' 카테고리의 다른 글
| [DirectX12 - Vector & Matrix] Chapter 06. Projection, Screen 변환 행렬 (0) | 2023.06.30 |
|---|---|
| [DirectX12 - Vector & Matrix] Chapter 05. World, View 변환 행렬 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 03. 행렬 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 02. 벡터 (0) | 2023.06.30 |
| [DirectX12 - Vector & Matrix] Chapter 01. 삼각함수 (0) | 2023.06.30 |




댓글